Part I. Highlights of Linear Algebra

https://math.mit.edu/~gs/learningfromdata/

Part I에는 $Ax=b$ , $Ax=\lambda x$ , $Av=\sigma u$ , factorization of $A$ , 그리고 $Minimize \frac{\|Ax\|^2}{\|x\|^2}$ 에 대해 다룬다. (1p) 다른 건 선형대수 수업에서도 봤던 내용인데 $Minimize \frac{\|Ax\|^2}{\|x\|^2}$ 는 뭔지 잘 모르는 상태로 시작했다.

I.1 Multiplication Ax Using Columns of A

2023.12.29

내용

$Ax$ 는 $A$ 의 column들의 linear combination이다. 이게 fundamental

행렬 A와 벡터 x에 대해 column들의 linear combination으로 보는 것이 더 higher level이고 이는 Column Space로 이어짐. (2p)
$Ax=b$ 에서 $b$ 가 column space 안에 있을 때 solvable하다는 것, (linearly) independent 의 정의, $R^3$ 에서 independent column 3개가 있으면 invertible이라는 것 복습 (3p)
rank는 independent column의 개수를 세는 것 (4p)
A=CR (5p)
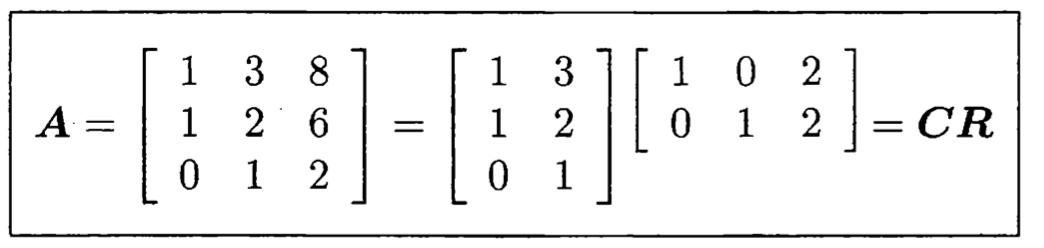
- $C$ 는 $A$ 의 column들 중 independent한 것들만 모은 것(이므로 A와 같은 column space를 가짐).
- 그리고 $R$ 은 $C$ 의 column들을 어떻게 조합해야 $A$ 가 나오는지에 대한 정보가 들어있는데, 이는 rref와 같음
- $A=CR$ $A = CR$ 은 Fundamental Theorem of Linear Algebra의 첫 번째 파트 중 dim(C(A)) = dim(C(A^T)) = r 을 증명할 수 있음. (5p)
  - $C$ 에 $R$ 을 곱하는 게 $C$ 의 column들을 조합하는 것이듯 R에 C를 곱하는 것은 $R$ 의 row들을 조합하는 것과 같음. 따라서 $R$ 의 row들은 $A$ 를 구성하는 것들이고 independent하기까지 하니 $C(A^T)$ 의 basis들임.
  - 그래서 $C$ 의 column이 $C(A)$ 의 basis, $R$ 의 row들이 $C(A^T)$ 의 basis인데 (곱하기를 하려면) $C$ 의 column 개수 = $R$ 의 row개수 이니까 FTLA가 증명된다고 하는 것이 아닐지..
- SVD는 A=CR에서 C가 orthogonal column 을, R이 orthogonal row를 가지는 경우. (5p)

Problem Set I.1

17, 18번

I.2 Matrix-Matrix Multiplication AB

2024.01.01 ~ 2024.01.02

내용

$AB$ = Sum of Rank One Matrices

$AB$ 는 row vector와 column vector의 outer product 여러 개의 합으로 볼 수 있다 (9~10p)
- 이 rank one matrix 역시 $C(A) = C(A^T)$ 의 예시가 됨 (10p)
- Matrix Multiplication을 inner product 방식으로 하든 outer product 방식으로 하든, $(m\times n)\times(n\times p)$ 의 경우에 $mnp$ 번의 곱셈을 하고, 곱셈하는 숫자들은 같은데 순서만 다름 (10p) - inner product 방식: $mp$ 번의 내적을 하는데, 그 각각에는 $n$ 번의 곱셈. 총 $mnp$ - outer product 방식: $n$ 개의 outer product가 있는데, 그 각각에는 $mp$ 번의 곱셈. 총 $mnp$

행렬 A를 CR로 분해 후 각 col*row들에 대해 아는 것은 A의 largest piece를 관찰하는 것 (11p)

5개의 중요한 factorization: $A=LU, A=QR, S=QΛQ^T, A=XΛX^{-1}, A=UΣV^T$ $A = LU, A = QR, S = Q Λ Q^{T}, A = X Λ X^{- 1}, A = U Σ V^{T}$ (11p)
- S와 Q는 선형대수의 King가 Queen (11p)
예시: $QΛQ^T$ 를 유도한 후 각 $\lambda qq^T$ 가 rank one piece 라는 것을 보여줌 (11~12p) 한양대 선형대수 수업 자료에서도 나온 적 있었던 부분. 이제 이해함

* $AB$ 중 $B$ 의 row들은 b*으로 표기함: $b^T$ 로 표기하지 않는 이유는, 그러면 $B$ 를 transpose했을 때처럼 $b^T$ 를 $B$ 의 column들로 오인할 수 있어서. (12p)

Problem Set I.2

2024.01.02

1,6,8번

I.3 The Four Fundamental Subspaces

2024.01.02

내용

4 Subspaces에 대한 예시 3개가 제시됨.

Example 2: subspace의 basis들은 perpendicular인 게 좋다는 점 제시 (14p)
Example 3: 행렬 예시 자체가 그래프의 incidence matrix
- element가 -1이면 그 노드가 start node, 1이면 그 노드가 end node라는 뜻
- $A$ 는 $m\times n$ 사이즈이며 m개의 edge와 n개의 node를 나타냄
- 아래의 column space와 left null space구할 땐 $A^T⋅y=0$ 으로 만드는 $y$ 에 대해 논하는데 (17p)
  
  dependent rows→ $A$ 에 $y$ 를 곱한 결과는 그래프로 보면 loop
  independent rows → $A$ 에 $y$ 를 곱한 결과는 그래프로 보면 tree
- $N(A^T)$ 를 구할 때
  - $A$ 에 $y$ 를 곱한 게 그래프로 보면 loop이 되는 $y$ 를 찾으면 → $A^T⋅y=0$ 을 만족 (17p)
    
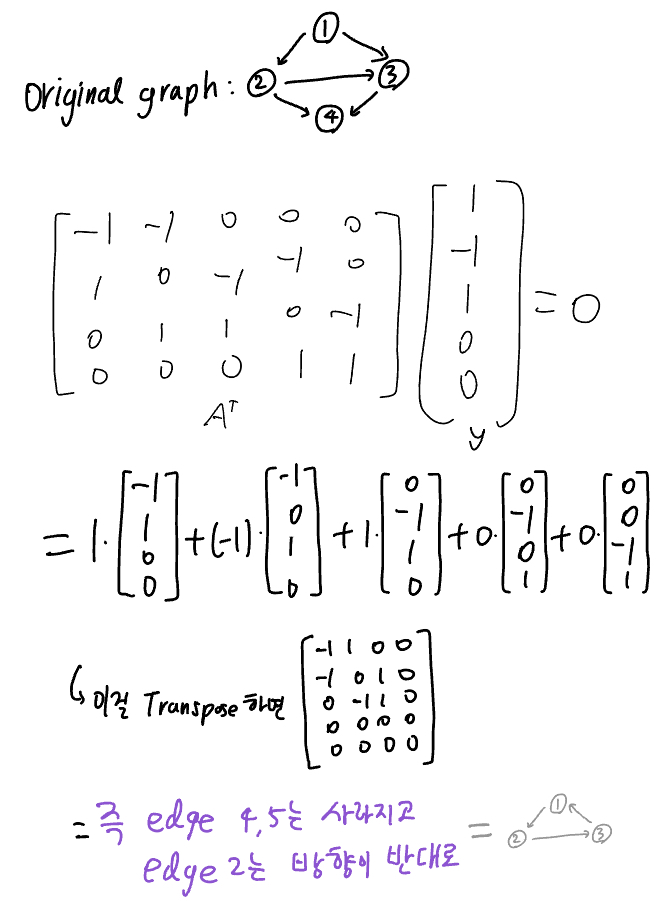
    이건 반대로 $A^T⋅y=0$ 인 $y$ 가 그래프에선 loop을 만든다는 순서로 풀어놓은 것이긴 함
- row가 서로 dependent인지 볼 때 elimination 말고 loop, tree로 보는 게 beautiful way (17p)
$AB$ , $A+B$ 의 Rank에 대한 증명들 (19p)

Problem Set

I.4 Elimination and A = LU

2024.01.03 3:00 AM

내용

선형대수의 most fundamental problem은 $Ax=b$ 를 푸는 것이라고 제시 (21p)
이 파트의 핵심은 elimination 과정을 rank 1 matrix들의 관점에서 보는 것 (21p)
- 각 elimination은 행렬lu*를 없애는 것이고, 그 rank one matrix들의 합이 $A$ .
LU 전에 2x2 $A$ 에 대해 $Ax=b$ 를 row picture로 보는 것부터 (Figure I.4) (21p)

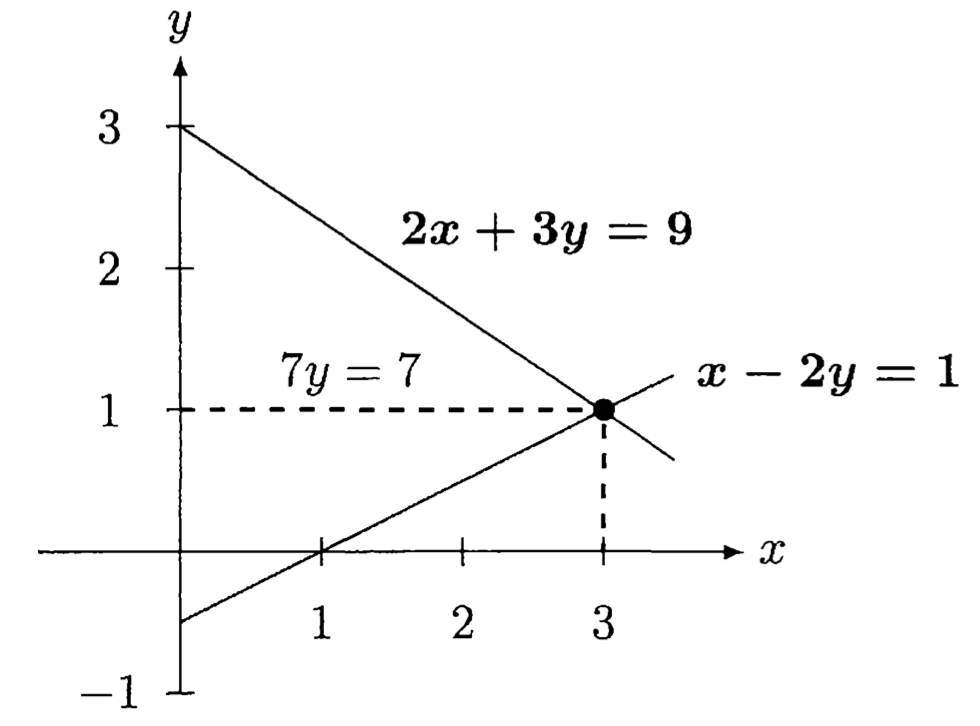
(column picture는 figure 생략)
$n \times n$ 에서 $n≥3$ 이면 column picture로 보는 게 더 편함 (22p)
23p 윗부분은 그냥 LU decomposition의 과정

LU decomposition의 key idea: Reduce the problem size from n to n-1 by elimination (24p)
LU decomposition 역시 n개의 rank one matrix들의 합으로 볼 수 있다! (23~24p)

25p 윗부분은 LU로 Ax=b 구하는 법 (c벡터 사용해서)
- → 하나의 square system이 두 개의 triangular system으로 바뀜 (25p)
pivot은 0이 아니어야 한다! a_11=0이면 다른 row가 pivot row가 될 수 있을텐데, Good codes will choose the largest number to be the pivot, even if a_11 is not zero 라고 함
PA=LU (26p)

Problem Set

I.5 Orthogonal Matrices and Subspaces

2024.01.03 10:00 PM

내용

* Orthogonal matrices 라 하면 square with orthonormal columns 라 하는데.. 사실상 Orthonormal matrices 라고 하는 게 맞다고 함(29p)

Orthogonal matrix $Q$ 에 대해 $\|Qx\|=\|x\|$ (29p)
30p부터는 orthogonal한 vector, basis, subspace, matrix의 예시가 나옴
- orthogonal basis와 Hadamard matrix (30p)
- orthogonal subspaces의 예시는 4 fundamental subspaces (31p)
- SVD is most important theorem in data science; 단순 Gram-schmidt로 $A$ 의 $C(A), C(A^T)$ 를 찾는 것과 달리, SVD는 $v$ 와 $u$ 가 $Av=\sigma u$ 의 관계로 이어질 수 있게 함 (31p)
- Left inverse, Right inverse (32p)
- Projection Matrix $P$ $P$ 에 대해 $Pb$ 는 $b$ 를 $P$ 의 column space로 proejct한 것 (32p)
  - $P^2=P$ 이면 $P$ 는 projection matrix인데, $Q$ 에 대해 $P = QQ^T$ 는 projection matrix임
    $\because P^2=(QQ^T)(QQ^T)=Q(Q^TQ)Q^T=QQ^T=P$
    그래서 orthonormal한 column들로 이루어진 $Q$ 로 project할 때는 $P=QQ^T$ 를 사용 (32p)
- orthogonal matrix 중에는 rotation matrix, reflection matrix도 포함 (33p)
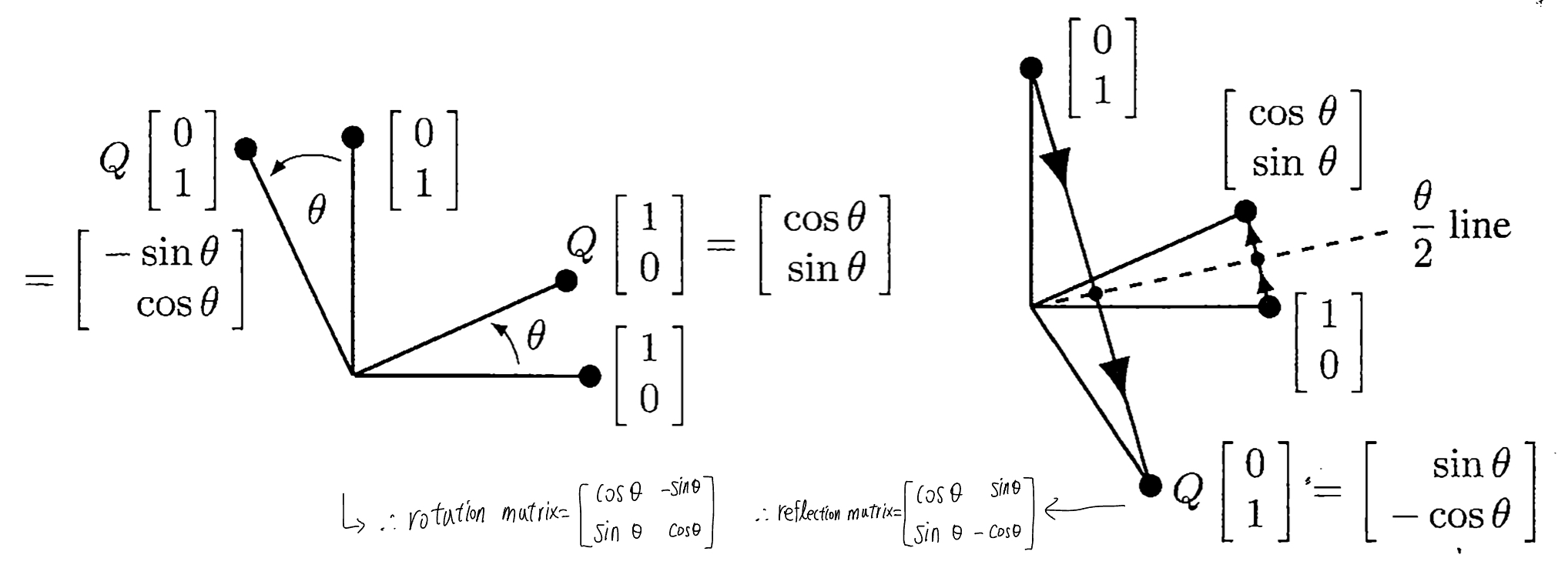
Orthogonal Basis = Orthogonal Axes in $R^n$
basis가 $q$ 이면 $v=c_1q_1+c_2q_2$ 의 $c$ 들을 separately 구할 수 있음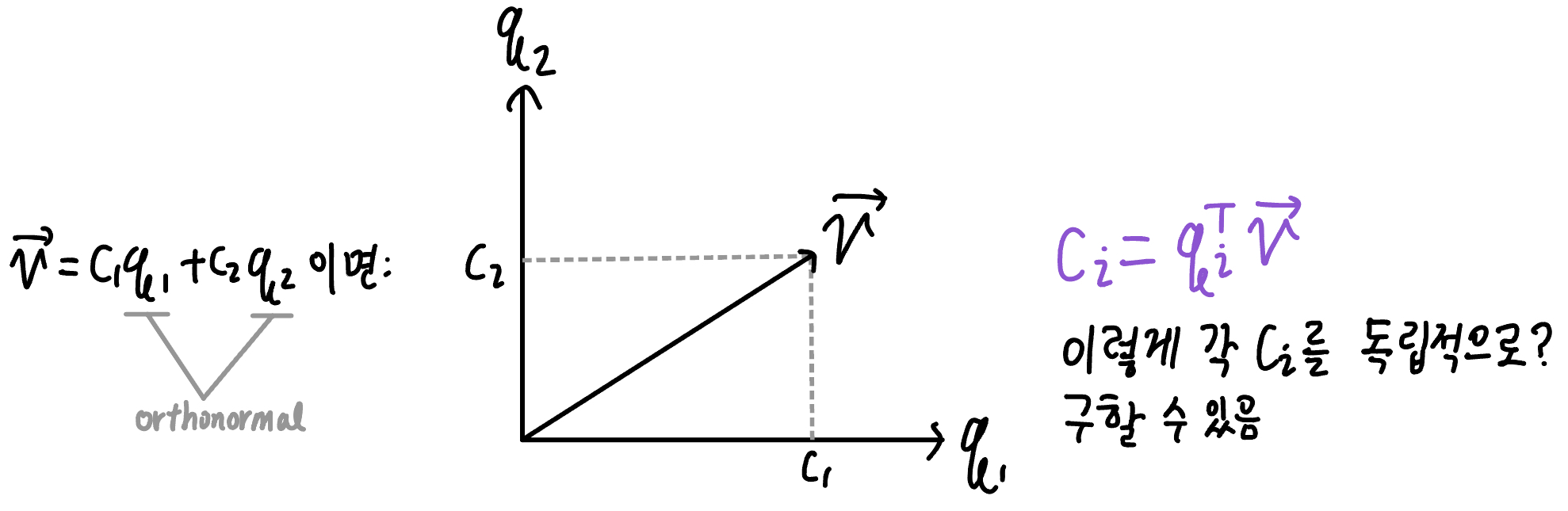
예시로 householder reflection (34p)

어휘..

hypotenuse
right triangle

Problem Set

1 (그냥 풀어봄), 4

I.6 Eigenvalues and Eigenvectors

2024.01.04 11:00 AM

내용

$n \times n$ 인 $A$ 에 $n$ 개의 eigenvector가 있을 때 $v = c_1x_1+...+c_nx_n$ 이다? (36p)
Similar matrix: $BAB^{-1}$ $B A B^{- 1}$ 은 $A$ $A$ 와 eigenvalue가 같다. (증명은 38p)
- 활용: $det(A-λI)$ 계산이 힘들 때 $BAB^{-1}$ 를 triangular로 만들어서 편하게 eigenvalue를 구함

(optional) Geometric Multiplicity, Algebraic Multiplicity로 diagonalizable 여부 판별하기 (40p)

Problem Set

I.7 Symmetric Positive Definite Matrices

2024.01.04 12:40 PM

내용

Symmetric Matrix의 특징: 1. real eigenvalue 2. can choose orthogonal eigenvectors. (44p)
Positive definite: powerful property that puts them at the center of applied mathematics
꼭 symmetric일 때만 해당되는 건 아닌 듯
positive definite이면 $AA^T$ 로 분해 가능 (90p)

positive definite인지 test하는 법 5가지:

Eigenvalue가 >0인지 열심히 확인
Energy-based definition: 가장 중요한 아이디어!! 이게 아래의 test들도 파생시킴 $energy = x^TSx>0\quad∀x≠0$ 이면 positive definite이다. (46p) 증명은 $Sx=\lambda x, \ \ x^TSx=\lambda x^Tx$ . 즉 $x^TSx>0$ 이려면 우변에서 $\lambda>0$ 이어야 함.
ex) $S_1, S_2$ 모두 positive definite이면 $S_1+S_2$ 도 positive definite임을 energy test로 쉽게 검증
$S=A^TA$ $S = A^{T} A$ 인데 $A$ $A$ 는 independent columns (dependent면 zero energy 유도 가능) (47p)
이게 Cholesky Decomposition이고, symmetric인 S에 대해 다음 방법 등으로 구할 수 있음
- $S=LDL^T$ 하고 나면 $A=\sqrt{D}L^T$
- $S=QΛQ^T$ 이니 $A=Q\sqrt{Λ}Q^T$
leading determinants(왼쪽 위에서부터 대각선으로 한 칸씩 확장) 모두 positive
elimination 후 모든 pivot들이 positive k-th pivot = $\frac{D_k}{D_{k-1}}$ (48p)

linear algebra의 positive definite matrix는 calculus의 minimum problem과 연결 가능 (49p)
- univariate일 때 특정 지점 $x_0$ 에서 $\frac{df}{dx}=0, \quad \frac{d^2f}{dx^2}>0$ 이면 minimum이듯
- multivariate일 때는 $(x_0,x_1,...,x_n)$ 에서 편미분값들=0, Hessian Matrix가 positive definite이면 최소. Hessian Matrix의 eigenvalue들을 비교하는 그 얘기 (49p)
- Hessian matrix의 eigenvalue들 중 양수 음수 다 있으면 saddle point 라는 건 미적2 기말고사 범위 첫 내용의 그것과 같은 듯 (50p)
- 또는 hessian이 positive definite(semidefinite)이면 함수는 convex, eigenvalue들이 특정 양수 $\delta$ 보다 크면 strictly convex
Optimization and Machine Learning: 이계도함수를 다 계산하는 건 어려움을 다시 강조 (50p)
The Ellipse: 시작에 앞서.. 49p부터 나오던 $[\begin{matrix} 5 & 4\\ 4 & 5 \\ \end{matrix} ]$ 의 energy function $E(x,y)$ 에 대해
$E(x,y)=5x^2+8xy+5y^2>0$ 이 bowl opening upwards라는 말은 3차원에서 봤을 때를 말함
$S=QΛQ^T$ 는 principal axis theorem이라고도 함; $q$ 벡터들을 구하면 그게 새로운 axis로 쓰일 수 있음. (Figure I.9)

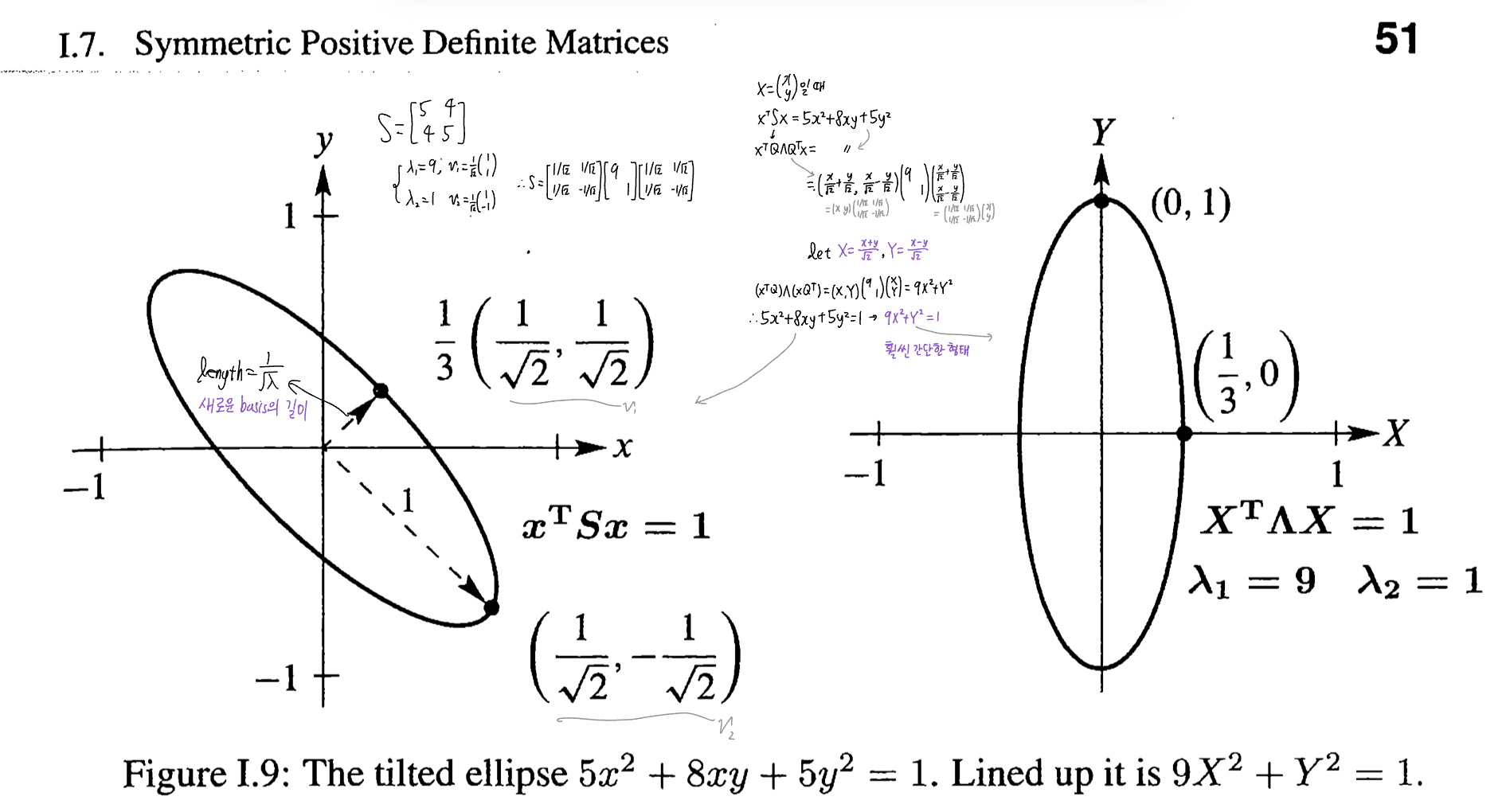
Problem Set

I.8 Singular Values and Singular Vectors in the SVD

2024.01.04 3:20 PM

내용

Reduced form of the SVD: rank 개수까지만 남긴 것 ((57p)
The Important Fact for Data Science: SVD도 다른 분해들처럼 행렬을 rank one pieces로 나누는데, SVD는 그 piece들이 중요한 순서대로 나타남. 첫 번째 piece $σ_1u_1v_1^T$ 가 가장 $A$ 와 가까움. (58p)
SVD 구하는 법과 proof가 있는데 읽고 넘김 (59p), 60p 예시도 생략

Q&A

$S$ 가 symmetric positive definite이면 $S=QΛQ^T=A=UΣV^T, \quad U=V=Q$ (61p)
$S=QΛQ^T$ 에서 negative eigenvalue가 있다면? → $σ$ 는 부호를 바꿔서 양수로, 대응하는 $u$ 는 부호를 바꿔서 음수로. (61p)
KL transform은 stochastic form of PCA (61p)
Geometry of SVD: $U,V$ 는 orthogonal matrix니까 rotation matrix로 볼 수 있다.(62p)

$V,Σ,U$ 순서로 rotate, stretch, rotate
$u_i,\sigma_i,v_i$ 를 하나하나 살펴보면 $maximize \frac{\|Ax\|}{\|x\|}$ 과 관련이 있음
1. 일단 maximize하는 $x$ 가 $v_1$ 이고, 이 때 $\frac{\|Ax\|}{\|x\|}=\sigma_1$ 가 나옴.
2. 그리고 저 다음으로 maximize하는 $x$ 를 찾기 위해 조건을 걸어서 $maximize \frac{\|Ax\|}{\|x\|}\quad s.t.\quad v_1^Tx=0$ 를 풀면 $x=v_2$ 임. $\frac{\|Ax\|}{\|x\|}=\sigma_2$ . (저 조건식 풀 때 lagrange multipler 사용)
3. 이런식으로 계속 찾다보면 (=ellipsoid의 axis들을 찾는) singular vector가 계속 나오는 것 (63p)
Singular vectors of $A^T$ : $A^Tu_k=\sigma_kv_k$ , 그냥 transpose 한 것 (64p)
A different symmetric Matrix also produces the SVD: $[\begin{matrix} 0 & A\\ A^T & 0 \\ \end{matrix} ]$ 로 한다는데 이건 무슨..? (64p)
$AB$ 와 $BA$ 는 같은 nonzero eigenvalue를 가진다: 그래서 $A^TA, AA^T$ 가 같은 singular value를 가짐 증명은 책에 있고.. (64p)
$maximize \frac{\|Ax\|}{\|x\|}$ 를 통해 $\|A\|=\sigma_1$ 라 했는데, 이를 통해 Submatrix B는 Matrix A보다 singular value가 더 클 수 없다는 것을 증명 가능. $\sigma_1(B)\le\sigma_1(A)$ 이고 $\|B\|\le\|A\|$ (65p)
SVD가 역사적으로는 행렬 말고 operator에 대해 먼저 나타났다고 함 (65p) $D(sinkt)=k(coskt)$ ← $Av=\sigma u$ 형태. ( $D$ =Derivative) - Derivative를 discrete하게 보면 finite differences이고 이로부터 $U,V$ 를 구하면 Discrete Sine Transform과 Discrete Cosine Transform을 얻을 수 있는데, 이게 JPEG기술의 핵심 (66p)
Polar Decomposition $A=QS=(UV^T)(V\Sigma V^T)$ (67p)

Problem Set

I.9 Principal Components and the Best Low Rank Matrix

2024.01.08 2:30 PM

내용

Principal Component라 함은 $U,V$ $U, V$ 의 column들인 $u_i, v_i$ $u_{i}, v_{i}$ 를 말하고, PCA는 가장 큰 $\sigma_i$ $σ_{i}$ 들과 연결된 $u_i, v_i$ $u_{i}, v_{i}$ 를 사용해서 데이터 행렬에 담긴 정보를 이해하고자 함 (71p)
- $S=Q\Lambda Q^T$ 에서도 $Q$ 의 column들이 principal component여서 그걸 축으로 썼던 것과 같을 듯

일단 $A$ 와 가장 가까운 rank k matrix는 $A_k$ 라는 것에서 (모든 것은) 시작된다. (몇 가지 증명들이 있음) (71p)
Matrix norm $\|A\|$ 중 다음과 같은 세 가지 유명한 게 있음 (71p)
- Spectral norm: $max\frac{\|Ax\|}{\|x\|}=\sigma_1$ (aka $L^2$ norm, 또는 induced norm. $A$ 를 $Av$ 즉 벡터로 만들어서 vector norm으로부터 matrix norm을 유도했으니까)
  $A$ 가 벡터 $x$ 를 가장 길게 늘일 수 있는 정도를 찾는 것. 근데 그 값이 $\sigma_1$ 인 걸 SVD로 이미 알고 있음.
  $Av_1=\sigma_1u_1$ 인데 $v_1,u_1$ 은 어차피 unit vector이니 $\sigma_1$ 의 값이 어떤 벡터를 가장 길게 늘린 수치.
- Frobenius norm: $\|A\|_F=\sqrt{\sigma_1^2+\sigma_2^2+...\sigma_r^2}$
- Nuclear norm: $\|A\|_N=\sigma_1+\sigma_2+...\sigma_r$
- orthogonal matrix $Q$ 의 $\sigma_i=1$ 이다 (71p)
- 위 3종류의 norm에 대해 $\|Q_1AQ_2^T\|=\|A\|$
Eckart-Young에 대해 알아보자. If $B$ has rank $k$ then $\|A-B\| \gt \|A-A_k\|$ ..라는데 예시로 보면 (72p)
- $A = \begin{bmatrix} 4 & 0 & 0 & 0\\ 0 & 3 & 0 & 0\\ 0 & 0 & 2 & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} $$ 일 때, rank 2 matrix 중 가장 A와 가까운 $$A_2 = \begin{bmatrix} 4 & 0 & 0 & 0\\ 0 & 3 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \end{bmatrix}$
  이다.
  
  Eckart-Young에 의해, ‘가장 값이 큰 두 수 4와 3을 남기자’ 하는 식으로 $A_2$ 를 선택하면 됨.
- 이 예시는 singular value가 4,3,2,1인 모든 $4 \times 4$ matrix에 대해 해당되는 이야기 ( $L^2$ norm과 Frobenius norm은 $\|Q_1AQ_2^T\|=\|A\|$ 이니까.. 라고)
- 참고로 위의 $A,A_2$ 에 대해 error를 측정하면 $L^2$ norm으로는 2, Frobenius norm으로는 $\sqrt{5}$
다른 rank 2 matrix $B_2$ 가 아닌, 어쨌든 $A_2$ 가 best라는 얘기를 $L^2$ norm과 Frobenius norm에 대해 증명하는 듯 한데 건너뜀.
PCA: statistics, geometry, linear algebra의 측면에서 봄 (75p) centered data A에 대해, SVD 중 S의 column인 $u_1$ 의 방향이 closest line to the centered data인 이유는?
- **The Statistics Behind PCA** (or algebra, 76p) 1. Covariance matrix $S=\frac{AA^T}{n-1}$ 의 원소들이 variance/covariance라는 것과 2. 그 Covariance matrix $S$ 의 eigenvectors
  note: 데이터 A로부터 symmetric한 S를 구해내는 것보다 A에서 바로 SVD하는 게 더 빠르고 정확
- The Geometry Behind PCA 이건.. 그냥 $u_1$ 방향의 line이 data point들과의 수직거리 합이 가장 작아진다는 뜻. 증명 생략 (77p)
- The Linear Algebra Behind PCA
  - 데이터의 Total Variance를 Frobenius norm과 연결 가능. 이는 분산과 singular value를 연결하고, 이를 이용하여.. (78p)
  $i$ 번째 principal component $u_i$ 가 전체 분산 T 중 $\frac{\sigma_i^2}{T}$ 만큼을 설명(explain)한다고 해석
  - Eckart-Young Theorem에 의해 k개의 singular vector를 사용하는 게 다른 어떤 k개 벡터들의 조합보다도 데이터를 가장 많이 설명해낼 수 있다는 것이 알려짐. (78p)
    예를 들어 아래 그림은 k=1, m=2(# of feature)
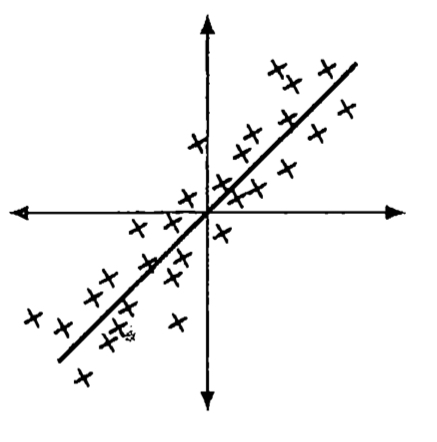
effective rank: 몇 개의 singular value를 사용할지에 대한. scree plot으로 찾을 수도 있고.. (78p)
rank of quarter circle one-zero matrix

Problem Set

I.10 Rayleigh Quotients and Generalized Eigenvalues

2024.01.09 12:25 AM, 2024.01.09 3:10 PM

내용

Rayleigh quotient $R(x) = \frac{x^TSx}{x^Tx}$ 에 대해 $R(x)$ 의 최댓값은 $x=q_1$ 일 때 $R(x)=\lambda_1$ . (eigenvalue 중 가장 큰 것. 반대로 eigenvalue 중 가장 작은 게 $R(x)$ 의 최솟값) $Sq_1=\lambda q_1$ 일테니 $R(x) = \frac{q_1^TSq_1}{q_1^Tq_1} = \frac{q_1^T\lambda_1 q_1}{q_1^Tq_1} = \lambda_1$ 이니까. (81p)
근데 $x=q_k$ 를 넣으면 그 지점들은 다 $R(x)$ 의 saddle points. (81p) 이건 왜 나온?
symmetric $S=A^TA$ 에 대해서 Rayleigh quotient는 A의 norm(의 제곱)과 같다. (81p) $\because ||A||^2=max\frac{||Ax||^2}{||x||^2}=max\frac{x^TA^TAx}{x^Tx}=max\frac{x^TSx}{x^Tx}=\lambda_1(S)=\sigma_1^2(A)$ 이걸 다르게 말하면, eigenvalue problem 역시 optimization임: Maximize R(x) (81p)

Generalized eigenvalues and eigenvectors: Applications in statistics and data science lead us to the next step.

Generalized symmetric eigenvalue problem이란: generalized rayleigh quotient $R(x)=\frac{x^TSx}{x^TMx}$ 와 같이 **symmetric matrix $M$ **이 추가될 때 $Sx=\lambda x$ 가 아닌 $Sx=\lambda Mx$ 를 다루는 것. (82p)
- $M$ : dynamical problem(역학 문제?)에선 mass/inertia matrix, statistics에선 covariance matrix.
- $Sx=\lambda Mx$ 에서 $H=M^{-1}S$ 로 두고 대입하면 $Hy=\lambda y$ 꼴이 나오고, 이 때의 $max \ R(x)=M^{-1}S$ (eigenvalue 중 가장 큰 것)이기는 한데.. 근데 이러면 $H$ 가 항상 symmetric이란 보장은 없음. (not really perfect, 82p)
- $H=M^{-\frac{1}{2}}SM^{-\frac{1}{2}}$ 이렇게 정의하면 eigenvalue들은 여전히 같은데도 $H$ 가 symmetric임! (82p) $M$ 이 positive definite이면 언제나 positive definite square root도 가진다 $M$ 은 symmetric이니까 $M=Q\Lambda Q^T$ 로 분해하면 $M^{-\frac{1}{2}}=Q\Lambda^{\frac{1}{2}}Q^T$ 로 구하면 됨. - 이제 $x=M^{-\frac{1}{2}}y$ 라고 두면, $\frac{x^TSx}{x^TMx}=\frac{y^T(M^{-\frac{1}{2}})^TSM^{-\frac{1}{2}}y}{y^Ty}=\frac{y^THy}{y^Ty}$ 가 돼서 $Hy=\lambda y$ 라는 ordinary symmetric problem으로 바꿀 수 있음. 그럼 $max \ \frac{y^THy}{y^Ty} = \lambda_1$ .
- 결국: $M$ 이 positive definite일 때 $max \ R(x)=M^{-1}S$ , which is largest eigenvalue.
- Example 1: 단순 계산. mechanical engineering이면 $\lambda$ 가 스프링의 frequency와 관련… (83p)
- Generalized eigenvector : symmetric이면 eigenvector끼리 orthogonal이듯, $Sx=\lambda Mx$ 로 확장하면 M-Orthogonal 이라는 개념이 나온다. (83p)
  
  $x_1^TMx_2=0$ (M-Orthogonal) if $Sx_1=\lambda Mx_1$ and $Sx_2=\lambda Mx_2$ and $\lambda_1\ne\lambda_2$
$M$ 이 positive semidefinite으로 not invertible인 경우에는 $x_1^TMx_2=0$ 이 될 수 있어서 $\$ frac{x^TSx}{x^TMx} $의 값이 **무한대**가 될 수 있음. 이 때$ M^{-\frac{1}{2}}$$과 $H$ 는 존재 불가.. (84p)
mathematical하게 보는 한 가지 방법은, $\alpha Sx = \beta Mx$ , $\lambda=\frac{\beta}{\alpha}$ 로 두고 케이스를 나누는 것. $\alpha=0$ 일 때 $\lambda$ 는 무한대거나 undetermined일 수 있는데, 데이터 샘플이 # of features보다 적을 때 발생. → 그래서 $M$ 이 추가된 경우까지 커버하기 위해 아래의 GSVD라는 것이 나옴
Generalized SVD: (85p) column 수가 같은 두 tall thin matrices $A$ 와 $B$ 에 대해 $A=U_A\Sigma_AZ, \ B=U_B\Sigma_BZ$ 로 분해. 이 때 $A^TA=Z^T\Sigma_A^TU_A^TU_A\Sigma_AZ=Z^T(\Sigma_A^T\Sigma_A)Z$ 와 같이 가능해서, $S=A^TA$ 와 $M=B^TB$ 모두 $Z$ 로 diagonalize 가능함.
Fisher’s Linear Discriminant Analysis (86p)
- PCA처럼 Dimensionality reduction을 위한 테크닉
- Fisher’s criterion이라고도 하는, Separation ratio라는 것이 있다. $m_1, m_2$ 가 population1, population2의 feature들의 mean값들을 모은 벡터일 때 $R=\frac{(x^Tm_1-x^Tm_2)^2}{x^T\Sigma_1x+x^T\Sigma_2x}=\frac{x^T((m_1-m_2)(m_1-m_2)^T)x}{x^T(\Sigma_1+\Sigma_2)x}$ 즉 $\frac{x^TSx}{x^TMx}$ 의 형태로 풀어낼 수 있음. 이 ratio 값을 가장 크게 하는 $x$ 값인 $v$ 를 찾으면 - $v$ 와 수직인 plane이 두 population을 분리하는 것이고 - $v$ 벡터 방향의 line을 사용해서 차원축소를 할 수도 있고 (맞나?)

Problem Set

I.11 Norms of Vectors and Functions and Matrices

2024.01.11 12:00 AM, 2024.01.11 3:30 PM, 2024.01.12 2:00 AM, 2024.01.13 8:16 PM, 2024.01.14 1:43 PM, 2024.01.15 3:00 PM

내용

vector에 대한 것이든, function에 대한 것이든, matrix에 대한 것이든.. norm은 두 성질을 공유함 (88p)
- rescaling: $\|ku\|=\lvert k \rvert \|u\|$
- triangle inequality: $∥u+v∥≤∥v∥+∥u∥$
- $v=0 \Longleftrightarrow \|v\|=0$ 도 조건으로
가장 중요한 세 가지 norm (88p)
- L2 norm: $\|v\|_2 = \sqrt{\lvert v_1 \rvert^2 + \lvert v_2 \rvert^2 + ... + \lvert v_n \rvert^2}$
- L1 norm: $\|v\|_1 = \lvert v_1 \rvert + \lvert v_2 \rvert + ... + \lvert v_n \rvert$
- max norm: $\|v\|_\infty=max \ of \ \lvert v_1 \rvert, ... , \lvert v_n \rvert$ ( $l^\infty$ norm이기도 함)
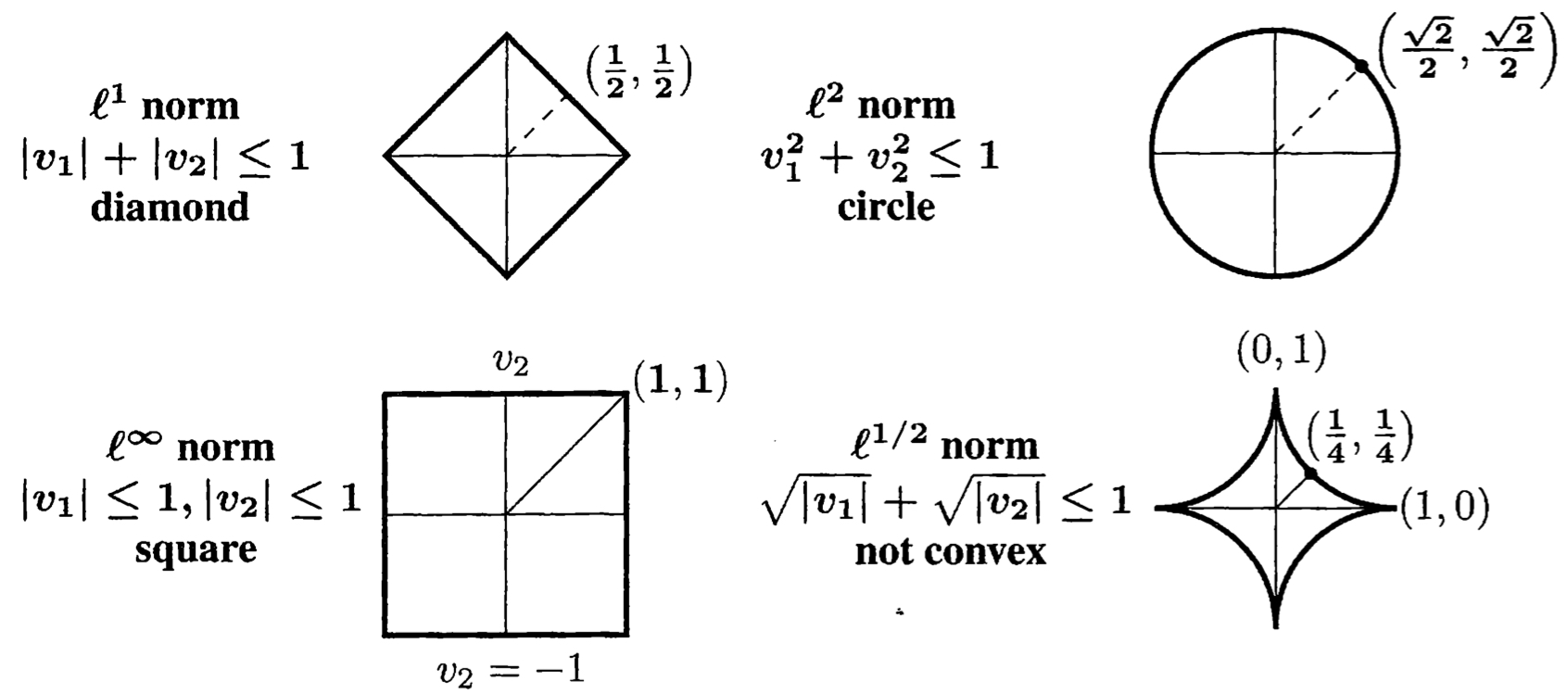
The Minimum of $\|v\|_p$ on the line $a_1v_1+a_2v_2=1$ (89p)**
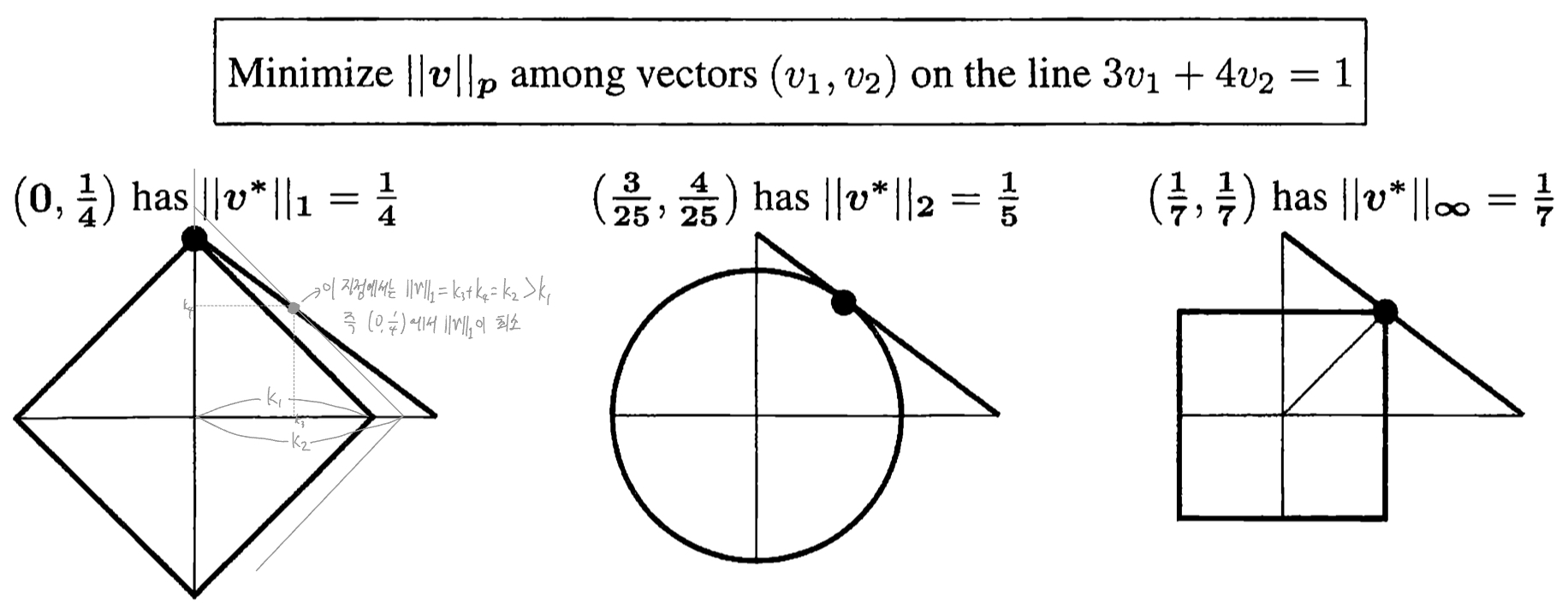
- L1 norm: solution vector $v^*$ 이 sparse함
L0 norm: zero norm=그 vector의 element들 중 nonzero인 것이 몇 개인가? (89p)
Inner Products and Angles (90p) Cauchy-Schwarz inequality와 triangle inequality는 most important inequalities in mathematics 그리고 L2 norm이 위의 두 inequality와 관련이 있음 (둘 다 dot product와 연관이 있으므로)
Inner Products and S-Norms (90p) 다른 norm과 연관시킬 수 있는 다른 inner product도 있음 positive definite matrix $S$ 에 대해 $\|v\|_S^2=v^TSv$ 를 S-norm이라 하고, $(v,w)_S=v^TSw$ 를 S-inner product라 하는 것. 그러면 $S=A^TA$ 이므로 $v^TSw=v^TA^TAw=(Av)^T(Aw)$ . 즉 weight된 벡터들의 내적. Einstein and Lorentz? (91p)
Norms and Inner Products of Functions (91p)
- function $f(x)$ 가 vector in function space이고 function간의 linear combination이 가능하다? vector를 함수처럼 쓰려는 게 핵심 아이디어
- vector의 element 개수가 무한한 infinite dimension일 때는 마지막 element들이 쭉 0이면 incomplete?
- Banach Space, Hilbert Space (91p) $\ell^1, L^1,\ell^{\infty}, L^{\infty}$ : Banach space, $\ell^2,L^2$ : Hilbert space
Smoothness of Functions (92p)
- function space $C[0,1]$ 이라 하면, $C[0,1]$ 은 구간 [0,1]에서 연속인 모든 함수들을 모은 것을 말함.
- function space $C$ $C$ 는 smoothness의 정도가 같은 함수들을 모음.
  - $C^n$ 은 1~n계 도함수가 연속인 함수들을 모은 것. $C^{\infty}$ 은 무한 번 미분 가능한 함수들을 모은 것.
  - 미적분학이나 기하학에서의 매끄러움은 $C^1$ 정도로 매끄러우면 된다. 즉, $f$ 가 미분 가능하고 $f'$ 이 연속이면 된다.
  - 해석학, 함수해석학에서는 매끄러운 함수란 (높은 확률로) $C^{\infty}$ 의 원소(인 함수)를 말한다.
- function space에서의 max norm $\|f\|_C=max \lvert f(x) \rvert$ ( $f$ 가 주어진 구간에서 연속일 때)
- $C^k$ norm: $\|f\|_{C^k}=\sum_{i=0}^{k}{\|f^{(i)}\|_{\infty}}$ 이고 $C^k$ norm은 Banach Space (+ not Hilbert space)
- $L^2$ space 기반으로 만들면 $\|f\|_{H_1}^2=\|f\|^2+\|\frac{df}{dx}\|^2$ 이렇게 Hilbert space $H^1$ 을 만들 수 있음
Norms of Matrices: The Frobenius Norm (92p)
- space of matrices는 vector space의 rule들을 다 따름. 따라서 matrix norm도 vector norm의 세 규칙을 따르고, 하나가 추가됨
  $\|A\|>0 \ when \ A\ne0 \ matrix, \|cA\|=|c|\|A\|,\|A+B\|\le\|A\|+\|B\|$ 그리고 $\|AB\|\le\|A\| \ \|B\|$ - 참고로 마지막의 경우 rank-1 matrix는 $\|ab^T\|=\|a\| \ \|b^T\|$ 로 등식이 됨
- orthogonal matrix $Q$ 에 대한 성질 복습: $\|Qx\|_2=\|x\|_2$ , $\|QB\|_F=\|B\|_F$ (93p)
  그래서 $\|U\Sigma V^T\|_F=\|\Sigma\|_F=\sqrt{\sigma_1^2+...+\sigma_r^2}$
  (이것 덕분에 $\|A\|_F=\sqrt{\sigma_1^2+...+\sigma_r^2}$ 가 유도되는 것. 심지어 $\|A\|_F^2=trace(A^TA)$ )
- trace를 이용해 Frobenius norm의 제곱은 그 행렬의 모든 원소 각각의 제곱의 합과 같음을 유도 가능
- matrix norm은 $A$ 를 $v$ 에 곱했을 때 얼마나 변화했는지, 즉 largest growth factor를 구하는 것
  - $\|Av\| \le \|A\| \ \|v\|$ 이런 식으로 식을 세우면 성립한다는 점 ( $\because ||A||$ 가 변화량 중 가장 큰 값, 즉 $||Av||$ 의 값들 중 가장 큰 것과 값은 값으로 고정된 값이고, $||Av||$ 는 $v$ 에 따라 변화하는 값이니까) 을 통해서도 $\|AB\|\le \|A\| \ \|B\|$ 증명 가능 (94p) 참고로 $\|Av\| \le \|A\| \ \|v\|$ 을 통해서 행렬의 $l^1, l^{\infty}$ norm 값을 유도함
  - $\|A\|_2, \|A\|_1, \|A\|_{\infty}$ 각각을 구하는 법은:
    - 이유는? l2 norm은 뭐 SVD고 (그래서 l2 norm의 값은 $U, V^T$ 에 영향을 받지 않음.) l1 norm:
      
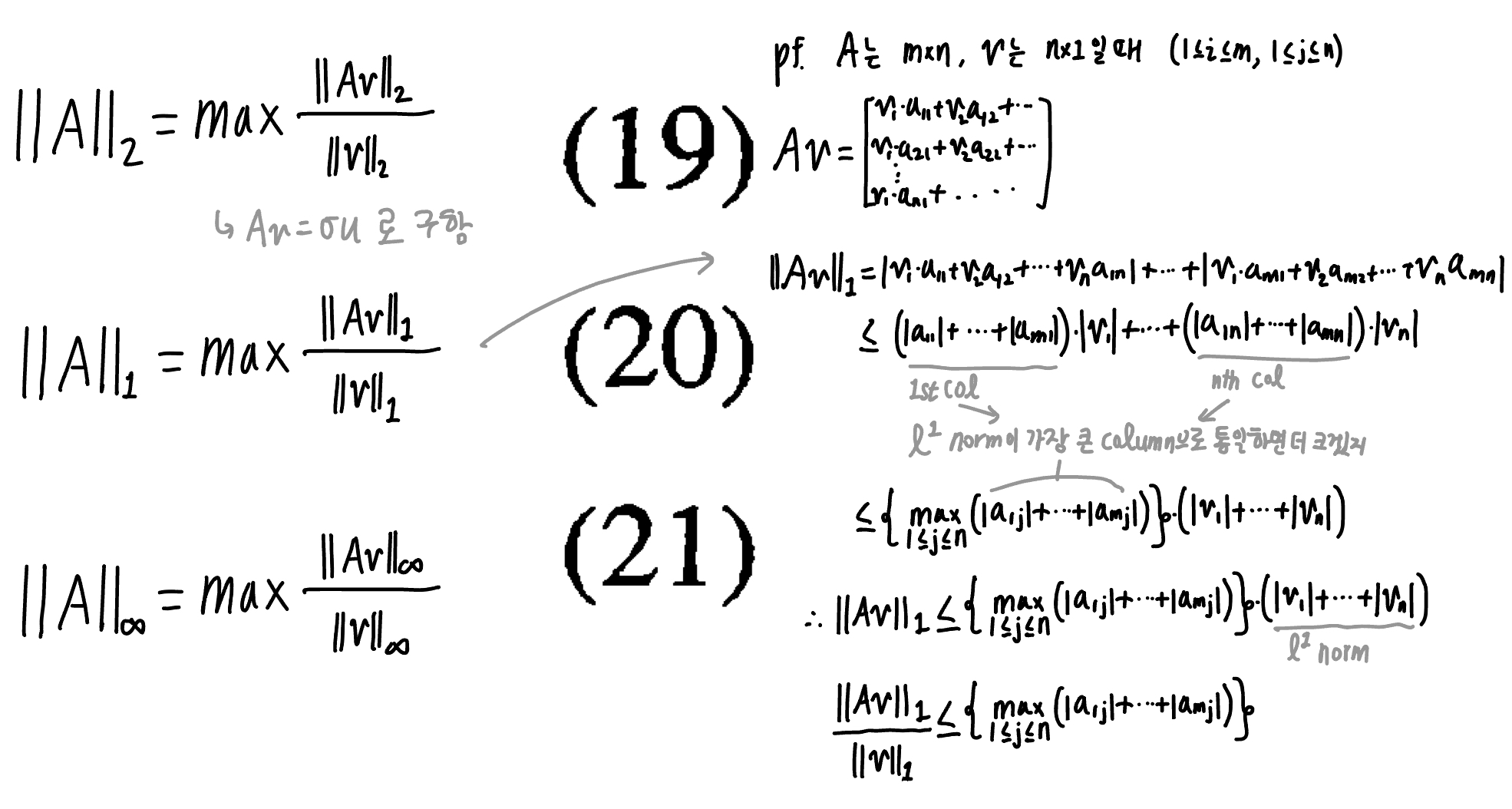
      l infinity norm은.. 생략
      l1, l infinity norm 구하는 법에 대한 증명 ^fn1
  - 아래 l1과 l infinity norm의 연관: $\|A\|_{\infty}=\|A^T\|_1$ , 이를 활용해 l1, l2, l infinity norm의 관계 유도 가능: $||A||_2^2=||A||_1 \ ||A||_{\infin}$ (94p)
The Nuclear Norm (trace norm) (95p) << I.9 에서도 나온 적 있음
- $\|A\|_{nuclear}=\sigma_1+...+\sigma_r$ .
- III.4에서 나오는 결측치가 있을 때의 matrix completion에서 nuclear norm이 key가 됨
- medical norm: $\lvert \lvert \lvert A \rvert \rvert \rvert _{\infty}$
Spectral Radius (95p)
- eigenvalue 중 가장 큰 것. $\lvert \lambda \rvert _{max}=max \lvert \lambda_i \rvert$ . norm의 조건은 충족 못함
- 이게 중요한 이유는 $\lvert \lambda \rvert _{max}<1$ 일 때 $\|A^n\|\rightarrow0$ 이기 때문

Problem Set

2024.01.15

I.12 Factoring Matrices and Tensors: Positive and Sparse

2024.01.15 5:18 PM, 2024.01.30 4:10 AM

내용

data matrix의 factorization에 대한 wider view를 제시

$A=U\Sigma V^T$ 만으로 충분하지 않을 수 있는 케이스: nonnegative, sparse, tensor data (97p)
- sparsity: nonzero인 수들에 의미가 있다는 걸 알 수 있음.
- nonnegativity: meaningful한 수를 찾기 위해. 아래 참고
- 그래서 위 둘은 very valuable properties라고 함(98p)
- 그런데 SVD를 하면 보통 +,- 부호가 섞여있는 작은 값의 수들이 매우 많게 됨.
$\Sigma$ 를 $U$ 로 합쳐서 $A=UV$ 로 분해하는 아이디어? k-means와도 관련이 있다고
Nonnegative Matrix Factorization (NMF): $A\approx UV$ (97p)
- 행렬 $A\ge0$ $A \geq 0$ 을 lower rank이면서 negative entry가 없는 두 행렬 $U\ge0,V\ge0$ $U \geq 0, V \geq 0$ 로 분해하는 것.
  - 참고로 $A\ge0$ 인 행렬의 예시는 98p의 얼굴 이미지 데이터. 이미지 각 픽셀의 intensity가 행렬의 element이니 각 값은 0이상.
  - 왜 lower rank? → simplicity
  - 왜 nonnegative? → meaningful한 숫자들을 만들기 위함. plus-minus cancellation 없는! (무게, 부피, 개수, 확률 같은 것들도 다 양수죠?)
- $A\ge0$ 이 symmetric positive definite이면? $A=B^TB$ 분해는 가능할텐데, 보통 $B$ 가 nonnegative로 존재하지는 않는다. 보통은 그냥 $A$ 와 가장 가까운 $B^TB$ 를 찾아야 함. (97p)
- practical하게는, $U$ 와 $V$ 의 orthogonality를 포기해야 함. (sparsity, nonnegativity를 더 중시, 98p)
- 이건 SVD와 달리 NP-Hard problem임 (99p)
SPCA $A\approx BC$ (98p)
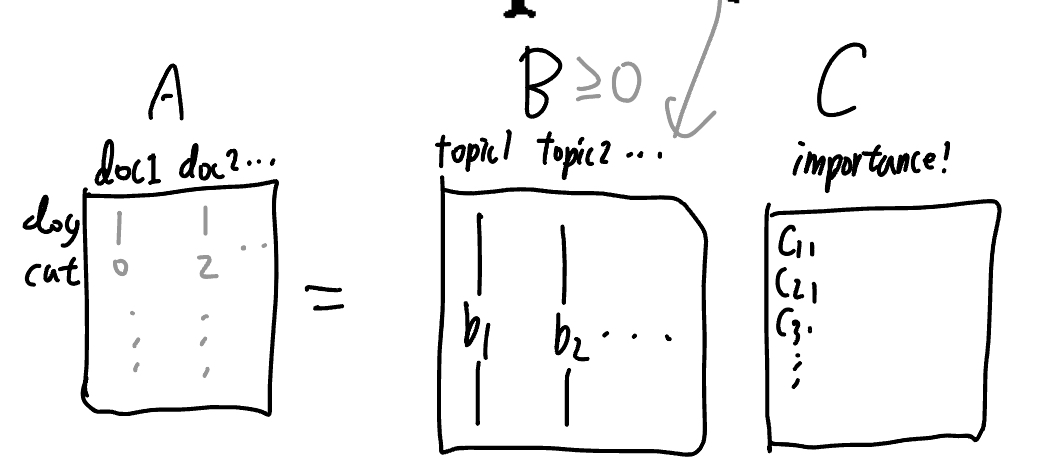
- $A\approx BC$ 를 찾는데.. $B,C$ 는 뭐 특별한 건 아님. $A$의 column $a_j=c_{1j}b_1+...+c_{nj}b_n$ 이니 이게 더 등식에 가까울수록 더 좋은 $B,C$ 인 것.
- $C$ 의 column 개수 < $A$ 의 column 개수이다? 그럼 dimensionality reduction.
- 이걸 쓰는 예시가 Facial feature extraction, Text Mining/Document Classification (98p)
Optimality Conditions (99p)
- $\|A-UV\|_F, \|A-BC\|_F$ 의 값을 minimize하는 게 중요한데.. 이 내용은 잘 모르겠는
Computing the Factors: Basic Methods (99p)
- 어쨌든 $U,V$ 또는 $B,C$ 를 어떻게 계산해서 구할지가 문제
- alternating factorization: 두 행렬 중 하나를 고정 후 다른 하나를 optimize, 그 후 반대로. 이걸 반복 Frobenius norm을 사용해서 각 단계는 least square의 형태가 됨
- 근데 이 방법은 convergence가 보장되지 않음. III.4에서 발전된 형태 ADMM이 나옴 (99p)
Sparse Principal Components (99p)
- nonzero component가 너무 많으면 다뤄야 할 변수가 너무 많다는 것인데.. 그래서 non zero component의 개수가 중요.
- 근데 SVD는 $u,v$ 안에 대부분의 숫자가 다 nonzero임. 값이 너무 작은 걸 없앨 수도 있겠지만, 그냥 sparse vector를 만드는 알고리즘들이 제안되었음.
- matrix $X$ 에 대해서는 $l^1$ norm 말고 nuclear norm $\|X\|_N$ 을 사용.
- $l^1$ + ridge regression
Tensors (101p)
- tensor는 row, column에 이어 tube추가
- Example 2 : $w=Av$ $w = A v$ 에서 $T_{ijk}=\frac{\partial w_i}{\partial A_{jk}}=v_k\delta_ij$ $T_{ijk} = \frac{\partial w _{i}}{\partial A _{jk}} = v_{k} δ_{i} j$ (101p)
  - 이 때 $Av$ 의 $A$ 는 딥러닝 레이어 하나의 weight matrix를 생각하면 됨.
- Example 3 : The Joint Probability Tensor (102p)
The Norm and Rank of a Tensor (103p)
- 3차원 텐서를 3-way tensor, tensor of order 3라 함
- Frobenius norm처럼 norm of T = $sum T^2_{ijk}=\|T\|^2$
- 텐서의 의미: 이것도 matrix처럼 linear operator가 되거나, RGB 이미지는 3-way, 영상은 4-way tensor.
- tensor의 factorization은 다루지 않고, rank of tensor도 간단하지 않음 (103p)
- Eckart-Young theorem이 있는 matrix와 달리, tensor는 어떤 tensor에 대한 best approximation이 존재하지 않음. 그럼에도 low rank tensor를 구하는 방법에는 CP, Tucker가 있음
CP Decomposition (104p)
- 여전히 핵심은 rank-1 tensor의 합으로 텐서 T를 approximate하는 것
- SVD와 달리 각각이 orthogonal하지 않음.
- NP-Hard
- 이것도 alternating algorithm 있음 (105p)
- 목표는 $T \approx a_1\circ b_1\circ c_1+...+a_R\circ b_R\circ c_R$
Matricized Form of a Tensor T (105p)
- CP Decomposition 하기 전에 tensor를 matricize하는 방법 소개
- 위의 각각이 $T_1, T_2, T_3$
The Khatri-Rao Product $A\odot B$ (105p)
- Kronecker product를 이용해서, $K \times R$ 과 $J \times R$ 을 곱하면 $JK \times R$ 이 나오는…
- column들이 $a,b,c$ 인 행렬을 각각 $A,B,C$ 라 하면 $T_1 \approx A(C \odot B)^T, T_2 \approx B(C \odot A)^T, T_3 \approx C(B \odot A)^T$ 와 같이 나타낼 수 있음
Computing the CP Decomposition of T (106p)
- $B,C$ 고정 후 $A$ 에 대한 least square 풀고, … , 를 반복. 자세한 과정 생략 (107p)
The Tucker Decomposition (107p)
- $T \approx \Sigma^{P}_{1} \Sigma^{Q}_{1} \Sigma^{R}_{1}g_{pqr} a_p \circ b_q \circ c_r$ .
- 이제는 Khatri-Rao 말고 Kronecker product 사용: $T_1 \approx AG_1(C \otimes B)^T$ , 역시 생략
Decomposition and Randomization for Large Tensors (108p) 생략

Problem Set

References

Strang, G. (2019). Linear Algebra and learning from data. Wellesley-Cambridge Press.