Home
Blog
Music
Photo

ODE/SDE, GBM 시뮬레이션

Tags:

ODE와 SDE의 형태 비교

2024.02.09

Color notation :
differential form
explicit formula

  • 미분방정식에 대해 공부할 때 거의 가장 처음으로 접하게 되는 ODE y′=yy'=y 의 해는 y=y0ety = y_0e^{t} 와 같이 나타낼 수 있다.

  • 그리고, 현재 시점에서의 가격이 B0B_0 인 자산의 이자율이 rr 일 경우 tt 시점이 지난 후의 가격은 Bt=B0ertB_t = B_0e^{rt} 라고 나타낼 수 있다. (continuous compound interest)

    • 이는 dBtdt=rBt\frac{dB_t}{dt} = r B_t , 또는 dBt=rBtdtdB_t = r B_t dt 라는 ODE(Ordinary Differential Equation)의 해로 볼 수 있다.

      dBtdt=rBt∫dBtBt=∫rdtln(Bt)=rt+CBt=ert+CBt=B0ert\begin{aligned} \frac{dB_t}{dt} & = r B_t \\ \int{\frac{dB_t}{B_t}} & = \int{r dt} \\ ln(B_t) & = rt + C \\ B_t & = e^{rt + C} \\ B_t & = B_0 e^{rt} \\ \end{aligned}

  • 이는 GBM의 SDE(Stochastic Differential Equation) dSt=μStdt+σStdWtdS_t = \mu S_t dt + \sigma S_t dW_t 를 풀면 St=S0e(μ−12σ2)t+σWtS_t = S_0 e ^ {(\mu - \frac{1}{2}\sigma^2)t + \sigma W_t} 라는 해가 나오는 것과 같은 형태.

Geometric Brownian Motion 시뮬레이션

2024.02.10

Geometric Brownian Motion은 다음과 같이 표현할 수 있다.

dSt=μStdt+σStdWtdS_t = \mu S_t dt + \sigma S_t dW_t
Differential form
St=S0e(μ−12σ2)t+σWtS_t = S_0 e ^ {(\mu - \frac{1}{2}\sigma^2)t + \sigma W_t}
Explicit formula

diffusion term σStdWt\sigma S_t dW_t 의 영향

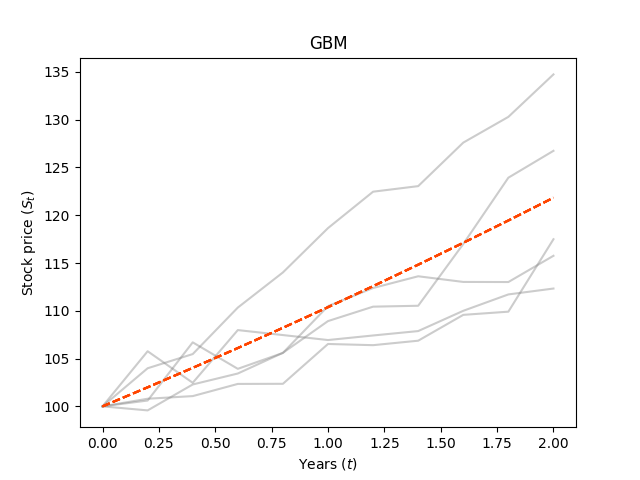
GBM_mu_0.1_sigma_0.05_years_2_N_5
$\mu=0.1, \sigma=0.05$
GGBM_mu_0.1_sigma_0_years_2_N_50
$\mu=0.1, \sigma=0$
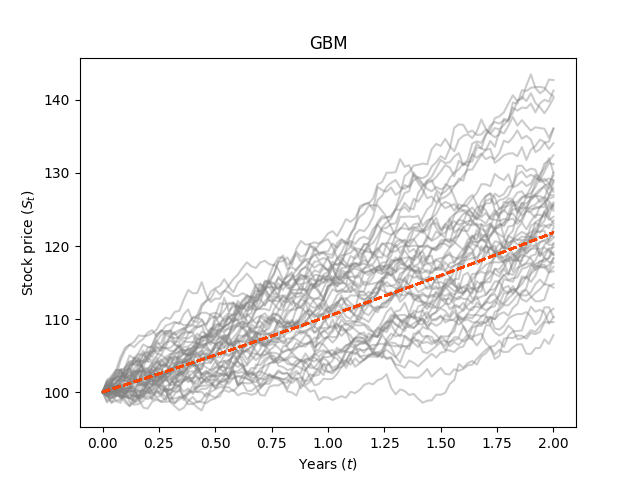
GBM_mu_0.1_sigma_0.05_years_2_N_50
$\mu=0.1, \sigma=0.05$
  • S0e(μ−12σ2)t+σWtS_0 e ^ {(\mu - \frac{1}{2}\sigma^2)t + \sigma W_t} 라는 식은 시간의 흐름에 따라 S0e(μ−12σ2)tS_0 e ^ {(\mu - \frac{1}{2}\sigma^2)t} 의 값을 가지되, 매번 예측할 수 없는 eσWte^{\sigma W_t} 만큼의 무작위성이 있다는 것으로 이해할 수 있다.
  • 따라서 GBM들은 S0e(μ−12σ2)tS_0 e ^ {(\mu - \frac{1}{2}\sigma^2)t} 의 그래프(빨간 점선)를 중심으로 한 값들을 가지게 된다.
    • 가장 왼쪽 그림과 같이 NN 값을 줄여서 보면, S0e(μ−12σ2)tS_0 e ^ {(\mu - \frac{1}{2}\sigma^2)t} 를 중심으로 한다는 것을 더 명확히 확인할 수 있다.
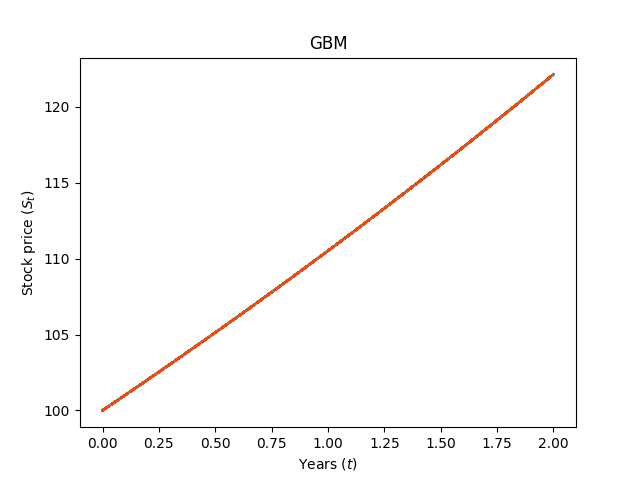
    • 그런데 σ=0\sigma=0 으로 diffusion term이 없게 된다면, 무위험자산과 동일하게 deterministic한 형태를 띄게 된다. 즉 시간의 흐름에 따른 예측이 정확히 가능하다. (두 번째 그림)
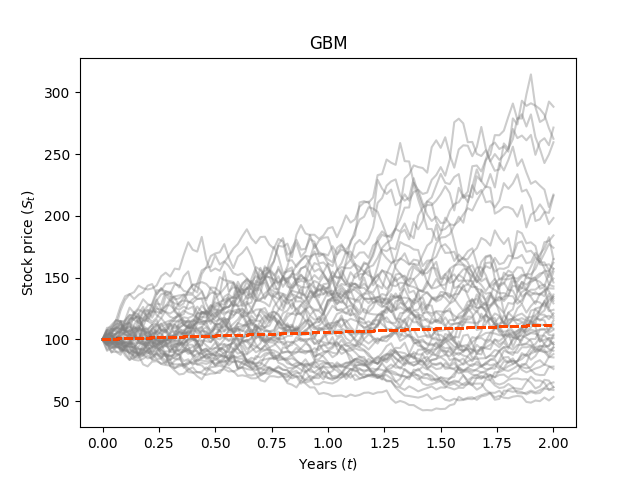
    • σ>0\sigma > 0 일 경우 무작위성이 쌓이며 S0e(μ−12σ2)tS_0 e ^ {(\mu - \frac{1}{2}\sigma^2)t} 의 그래프에서 점점 멀어지게 된다. (세 번째 그림)

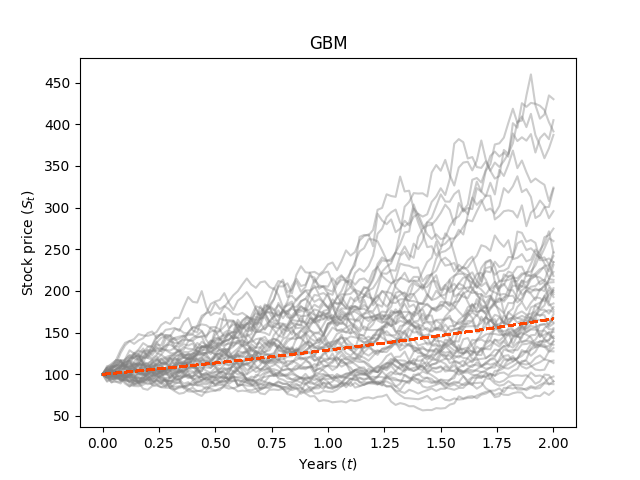
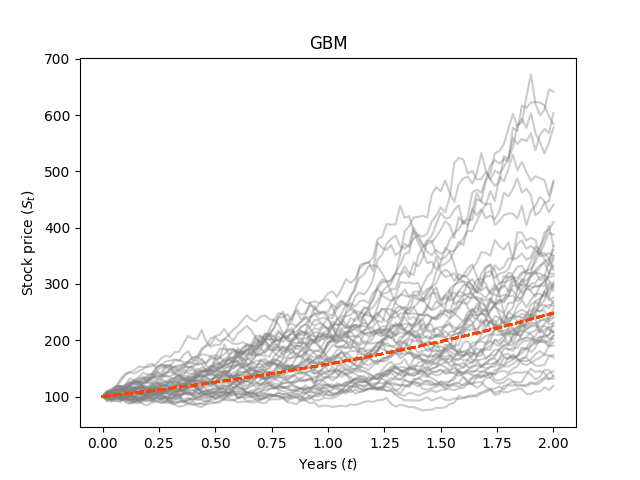
μ\mu 의 역할

GBM_mu_0.1_sigma_0.3_years_2_N_50
$$\mu=0.1, \sigma=0.3$$
GBM_mu_0.3_sigma_0.3_years_2_N_50
$$\mu=0.3, \sigma=0.3$$
GBM_mu_0.5_sigma_0.3_years_2_N_50
$$\mu=0.5, \sigma=0.3$$

μ\mu 값은 S0e(μ−12σ2)tS_0 e ^ {(\mu - \frac{1}{2}\sigma^2)t} 그래프의 형태를 바꿀 수 있으므로, 이를 이용해 trend를 조정할 수 있다.

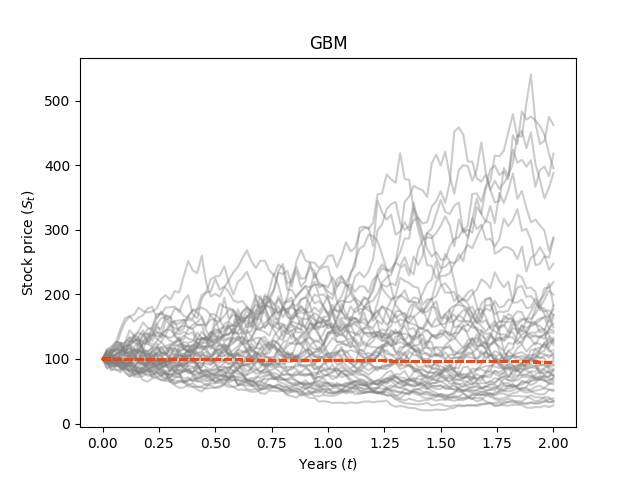
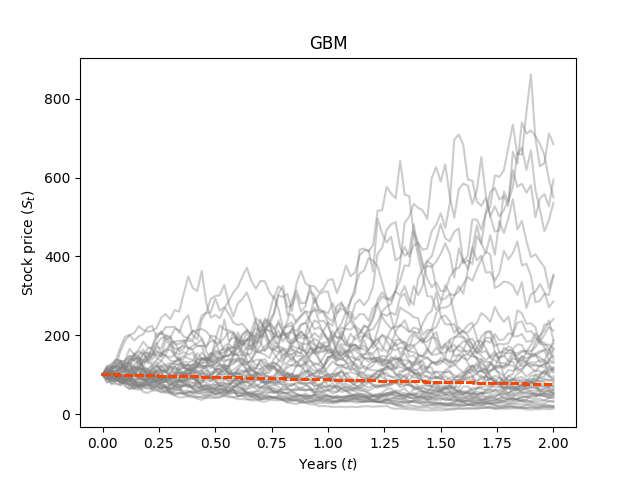
σ\sigma 의 역할

GBM_mu_0.1_sigma_0.3_years_2_N_50
$$\mu=0.1, \sigma=0.3$$
GBM_mu_0.1_sigma_0.5_years_2_N_50
$$\mu=0.1, \sigma=0.5$$
GBM_mu_0.1_sigma_0.7_years_2_N_50
$$\mu=0.1, \sigma=0.7$$

σ\sigma 값이 커질수록 S0e(μ−12σ2)tS_0 e ^ {(\mu - \frac{1}{2}\sigma^2)t} 의 그래프에서 멀어짐을 확인할 수 있다.

(μ,σ\mu, \sigma 에 상수가 아닌 함수를 넣는 건 나중에... Heston Model, Stochastic Volatility 등 참고)

코드

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(1)

### Parameters
MU = 0.1     #    drift coefficient
SIGMA = 0.5  #    diffusion coefficient

T = 2       #    time in years
N = 50      #    # of steps
M = 50      #    # of simulations

S_0 = 100    #    initial price


### Simulating GBM paths
dt = 1/N
S_t = np.exp(
    (MU - SIGMA ** 2 / 2) * dt                                       # drift term
    + SIGMA * np.random.normal(0, np.sqrt(dt), size=((N * T),M))     # diffusion term
)

S_t = np.vstack([np.ones(M), S_t]) # ((N * T) x M)
S_t = S_0 * S_t.cumprod(axis = 0)


time = np.linspace(0, T, T * N + 1)
tt = np.full(shape=(M, (T*N)+1), fill_value = time).T
plt.plot(tt, S_t, color='gray', alpha=0.4) # plot GBMs

drift_t = S_0 *  np.exp((MU - SIGMA ** 2 / 2) * tt.T[0]) # e^{(μ-σ^2/2)*t}
plt.plot(tt, drift_t, linestyle = '--', color = 'orangered') # plot drift

### Plot
plt.xlabel('Years $(t)$')
plt.ylabel('Stock price $(S_t)$')
plt.title(f'GBM')
plt.show()

### Info
print(f'{T} years')
print(f'{N} steps')
print(f'mu = {MU}')
print(f'sigma = {SIGMA}')

GBM StS_t 의 분포

  • Brownian motion의 정의에 따라 TT 시점에서 WT∼N(mT,σ2T)W_T \sim N(mT, \sigma^2 T) 이다. 다만 보통은 Browian motion / Wiener Process를 정의할 때 m=0,σ2=1m=0, \sigma^2=1 로 하여 WT∼N(0,T)W_T \sim N(0, T) 라고 본다.
  • GBM은 TT 시점에서 ln(STS0)=(μ−12σ2)T+σWTln(\frac{S_T}{S_0}) = (\mu - \frac{1}{2}\sigma^2)T + \sigma W_T 이므로, t=0t=0 시점부터 t=Tt=T 시점까지의 로그수익률은 ln(STS0)∼N((μ−12σ2)T,σ2T)ln(\frac{S_T}{S_0}) \sim N((\mu - \frac{1}{2}\sigma^2)T , \sigma^2 T ) 이다.

기타

  • 일일 변동성에 252\sqrt{252} 를 곱해서 연간 변동성을 계산하는 것도 WT∼N(mT,σ2T)W_T \sim N(mT, \sigma^2 T) 를 통해 생각해볼 수 있다. 표준편차(변동성)는 T\sqrt{T} 에 비례한다.

References

https://youtu.be/jejjUPfaIXY?si=Dn7o1IAXv2Mlymn8 https://sine-qua-none.tistory.com/238 https://blog.naver.com/chunjein/100154159130