Bayesian Game

Bayesian Game

---

• Extensive Form Game을 통해 Imperfect information이 존재하는, 즉 하나의 information set에 여러 개의 노드가 존재하는(=player가 상대방의 이전 action을 모르는) game을 다뤘다.
• 이번에는 Incmplete information이 존재한다. 각 player들에게 Type이라는 새로운 속성이 생긴다.
  • 각 유저들의 type을 나타내는 새로운 component $T = \{ T_i \}_{i \in N}$ 를 도입하게 되고
  • payoff는 $u: S \times T \rightarrow \mathbb{R}^n$ 와 같이 표현할 수 있다.

Bayesian Nash Equilibrium (BNE)

• 각 player들은 자신의 type에 따라 strategy를 잘 선택해서($\sigma_i^* : T_i \rightarrow \Delta(S_i)$) Expected utility를 극대화한다.
• 이 때 Expected Utility $\mathbb{E}[u_i(\sigma_i, \sigma_{-i}^*(t_{-i}), t) \vert t_i] = \sum_{t_{-i} \in T_{-i}} p(t_{-i} \vert t_i) u_i(\sigma_i, \sigma_{-i}^*(t_{-i}), t)$
  • 아래 Cournot Competition 예시가 이 수식을 이해하기 좋았다.

Example (Cournot Competition)

기업1, 기업2의 Marginal Cost는 각각의 type $T_i \in \{H, L\}$에 따라 $c_i \in \{c_i^H, c_i^L\}$ 이다. 두 기업은 각자의 생산량 $q_i^H \in [0, \infty), q_i^L \in [0, \infty)$ 을 결정하고, payoff는 $q_i(1-Q-c_i)$ 이다. ($Q=q_1+q_2$) 두 기업은 동시에 생산량을 선택한다(=static). 다음의 확률은 주어져있다고 하자.

• $p(c_1^H, c_2^H), p(c_1^L, c_2^L) = \frac{1}{2}\alpha$ $\quad$
• $p(c_1^H, c_2^L), p(c_1^L, c_2^H) = \frac{1}{2}(1-\alpha)$ $\quad$

그럼 두 기업이 각각 $H, L$의 타입일 경우에 따라 4가지의 payoff를 계산할 수 있다.

1. 기업1이 $H$ type인 경우, 기업1의 payoff

   $\mathbb{E}_1[u_1(\sigma_1, \sigma_2^*(t_2), t) \vert t_1=H] = \sum_{t_2 \in T_2} p(t_2 \vert t_1=H) u_1(\sigma_1, \sigma_2^*(t_2), t)$ 이다.

   $t_2 \in \{ H, L \}$ 이므로 위 시그마는 두 가지 경우에 대해 풀어내면 된다.

   $\mathbb{E}_1[u_1(\sigma_1, \sigma_2^*(t_2), t) \vert t_1=H] = p(t_2=H \vert t_1=H) u_1(\sigma_1, \sigma_2^*(t_2=H), t) + p(t_2=L \vert t_1=H) u_1(\sigma_1, \sigma_2^*(t_2=L), t)$

   위 식의 $p(t_2=H \vert t_1=H), p(t_2=L \vert t_1=H)$ 는 Bayes' rule로 구하면

   • $p(t_2=H \vert t_1=H) = \frac{p(t_2=H, t_1=H)}{p(t_1=H)} = \frac{p(t_2=H, t_1=H)}{p(t_1=H, t_2=H)+p(t_1=H, t_2=L)} =\frac{\frac{1}{2}\alpha}{\frac{1}{2}\alpha+\frac{1}{2}(1-\alpha)} = \alpha$

   • $p(t_2=L \vert t_1=H) = \frac{p(t_2=L, t_1=H)}{p(t_1=H)} = \frac{p(t_2=L, t_1=H)}{p(t_1=H, t_2=H)+p(t_1=H, t_2=L)} = \frac{\frac{1}{2}(1-\alpha)}{\frac{1}{2}\alpha+\frac{1}{2}(1-\alpha)} = (1-\alpha)$

   이제 대입해서 payoff를 극대화하는 optimization 식을 써내면

   $\underset{q_i^H}{max} = \alpha(1-(q_2^H+q_1^H)-c_1^H)q_1^H + (1-\alpha)(1-(q_2^L+q_1^H)-c_1^H)q_1^H$

   이고, 여기에 FOC를 적용하면

   $q_1^H=\frac{1}{2}(1 - \alpha q_2^H - (1-\alpha)q_2^H - c_1^H)$

   이 나온다.

2. 기업1이 $L$ type인 경우, 기업1의 payoff

   $\mathbb{E}_1[u_1(\sigma_1, \sigma_2^*(t_2), t) \vert t_1=L] = \sum_{t_2 \in T_2} p(t_2 \vert t_1=L) u_1(\sigma_1, \sigma_2^*(t_2), t)$ 이고, 다음 과정들은 모두 동일하다.

3. 기업2가 $L$ type인 경우, 기업2의 payoff

4. 기업2가 $L$ type인 경우, 기업2의 payoff

이렇게 4개의 식을 도출해내면, 미지수의 개수가 $q_1^H, q_1^L, q_2^H, q_2^L$ 4개이므로 해를 구할 수 있다.

Example (Cutoff strategy)

일단 생략

Example (Auction)

일단 생략

Harsanyi Transformation

player의 type이 확률적으로 결정되는 경우에, 이에 대해 Nature를 도입하여 모델링할 수 있다. player가 하나 늘어난 것과 같은 모양새가 된다.

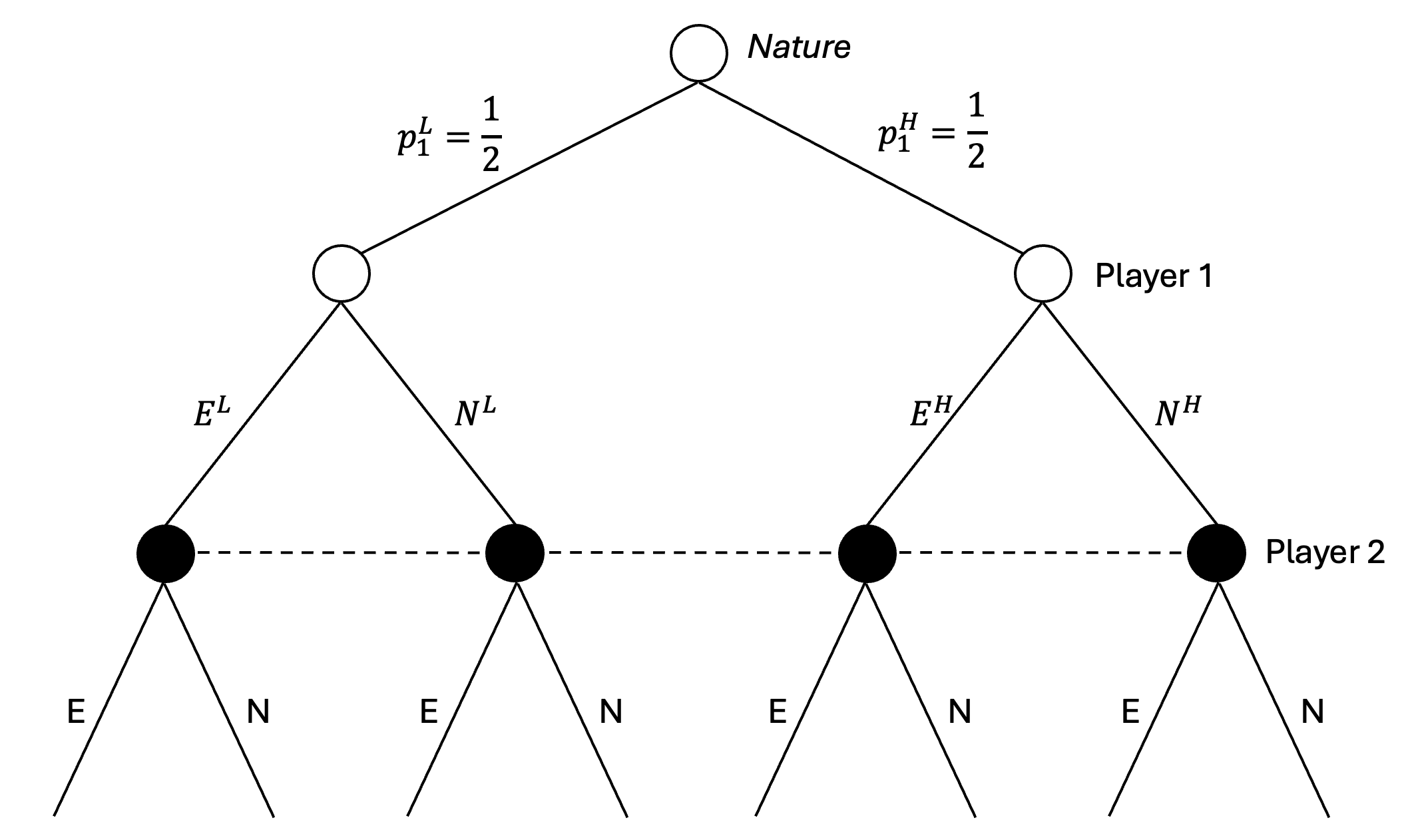
Example (Entry game)

2024.06.23