Weak Perfect Bayesian Equilibrium

Motivation: Subgame Perfect Nash Equilibria 중 dominated strategy를 포함하는 경우가 생길 수 있다.

Example

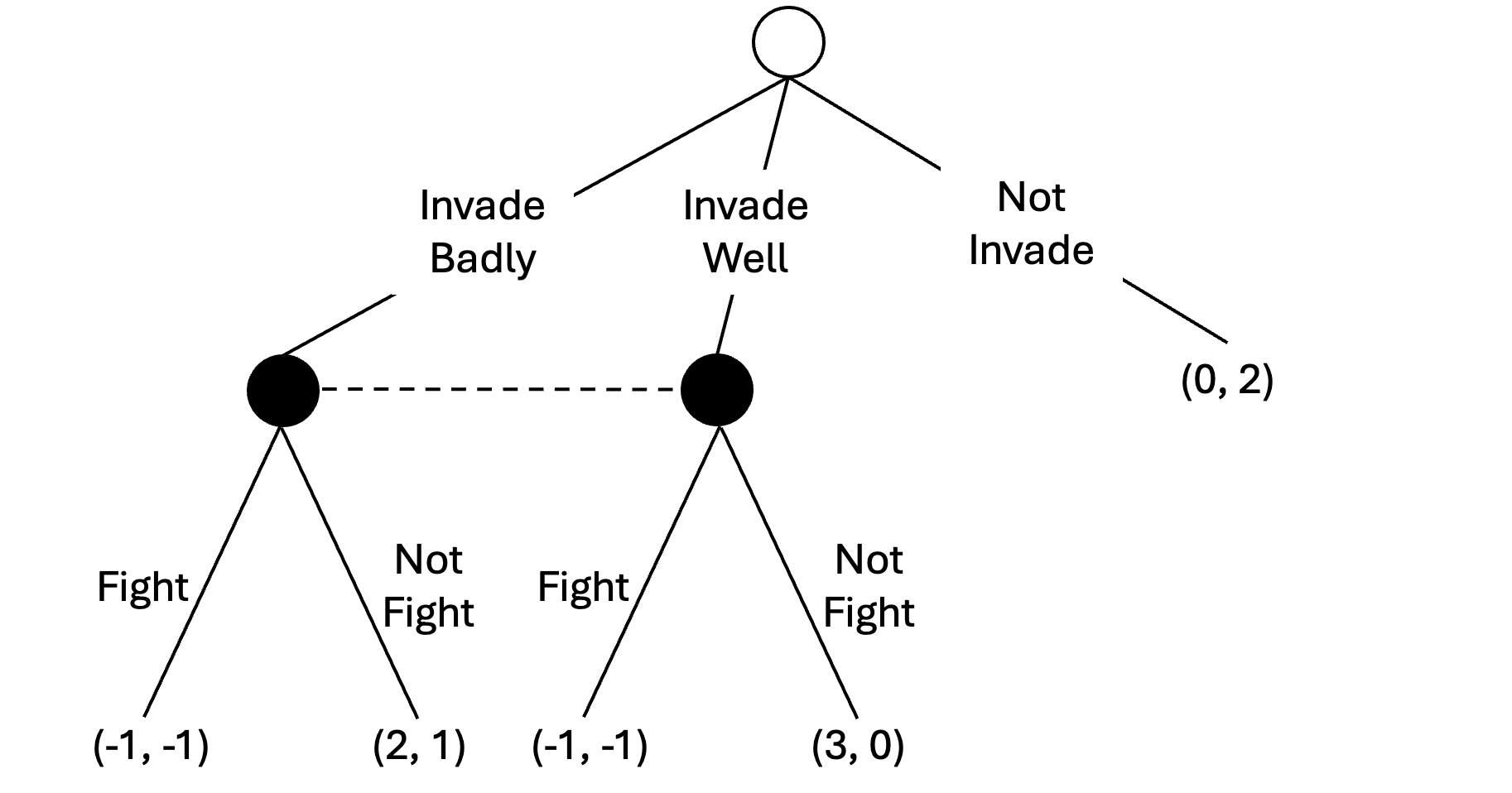
위 게임을 Normal form game 형태로 나타내서 N.E.를 찾으면 $(NI, F)$ 와 $(IW, NF)$ 가 나오고, 동시에 이 둘은 SPNE이다. ( $\because$ subgame이 한 개이므로)
그런데 $P2$ 의 입장에서 $F$ 는 dominated strategy이다. 이 $F$ 가 포함된 N.E. $(NI, F)$ 를 제외할 방법이 필요하다.

Definition (System of Beliefs)

먼저 이 개념이 필요하다. 게임에 존재하는 Imperfect Information에 대해 더 디테일하게 다루기 위한 개념이다.

Definition
Information Set $H$ 의 각 노드에 대해 확률값을 부여한 확률 분포를 System of Beliefs $\mu$ 라고 한다.

이로 인해 이제는 strategy의 차이에로만 Equilibrium 여부가 갈리는 것이 아닌, 상황에 대한 인식 차이에서도 Equilibrium 여부가 갈리게 된다. 즉 (지금까지도 그래왔듯) 더 많은 조건을 걸어서 더욱 specific한 상황에만 적용되는 Equilibrium을 찾을 것이다.

Definition (Weak Perfect Bayesian Equilibrium)

사실 위의 문제를 해결하기 위한 추가 조건은 간단하다. 각 N.E.에 대해 sequentially rational한지 여부만 한 번 더 따져주면 된다. (=각 N.E.에 대해, 각 player가 그 strategy를 선택하는 것이 더 이득이 맞는지 일일이 따진다.) 여기에 위의 system of beliefs를 합쳐 WPBE를 정의한다.

$\sigma^*$ 와 $\mu$ 에 대해 $(\sigma^*, \mu)$ 는 다음의 조건을 만족할 경우 Weak Perfect Bayesian Equilibrium이다.

$\sigma^*$ 는 $\mu$ 에 대해 sequential rational 하다.

(Wherever possible,) $\mu$ 는 strategy profile $\sigma^*$ 로부터 Bayes' rule로 유도 가능하다. (= consistent belief)

예시는 다음 내용인 Sequential Equilibrium 이후에 한 번에 보아도 될 듯 하다.

2024.07.03