Home
Blog
Music
Photo

How t-test works

Tags:
Gamma DistributionChi-Squared Distributiont Distribution가설 검정

올해 초에 OLS estimator의 분포와 t-test에 대해 정리한 적이 있었는데, 당시에는 왜 그런 과정을 거쳐 기각 여부를 결정하는지, t-statistic이 따르는 분포는 어떻게 유도되는 것인지에 대해 하나하나 뜯어보지 않고 넘어갔다. 이번에는 t-test가 왜 그런 과정을 거쳐서 기각 여부를 결정하는지에 대해 더 고민해보고, 그에 대해 이해할 때 필요한 여러가지 확률 분포들에 대해 정리했다.

Gamma Distribution

Definition (Gamma Function)

Γ(z)=∫0∞tz−1e−tdt\Gamma(z)=\int_0^{\infty}t^{z-1}e^{-t}dt

감마 함수는 팩토리얼을 복소수 범위까지 확장하는 함수로, 특히 자연수 nn에 대해 Γ(n)=(n−1)!\Gamma(n)=(n-1)! 이다.

Definition (Gamma Distribution)

f(x;α,β)=xα−1e−x/ββαΓ(α)f(x;\alpha,\beta)=\large{\frac{x^{\alpha-1}e^{-x/\beta}}{\beta^{\alpha}\Gamma(\alpha)}}

  • 감마 함수에 기반한 연속 확률 분포이고 x>0x>0에서 정의된다.
  • 감마 분포를 이용한 모델링의 예시에는 무엇이 있는지도 공부해야겠지만, 이건 이 포스트의 주제에서는 벗어나니 나중에 해보는 걸로...

Definition (Chi-Squared Distribution)

f(x;k)=xk/2−1e−x/22k/2Γ(k/2)f(x;k)=\large{\frac{x^{k/2-1}e^{-x/2}}{2^{k/2}\Gamma(k/2)}}

  • 감마 함수에 α=k2,β=2\alpha=\frac{k}{2}, \beta=2를 대입하면 카이제곱 분포가 된다. kk는 자유도(degree of freedom).
  • Z∼N(0,1)Z \sim N(0,1) 일 때 Z2Z^2가 따르는 분포가 무엇인지 유도하면 자유도가 1인 카이제곱 분포, χ2(1)\chi^2(1)이 된다.
  • 그리고 카이제곱 분포에는 additivity가 있다. 즉 ∑i=1nZi2∼χ2(n)\sum_{i=1}^n Z_i^2 \sim \chi^2(n)이다.
    • 왜 additivity가 있는지에 대한 증명은 아직 모름
  • 정규분포를 따르는 확률변수를 제곱한 것에 대한 분포, standard error의 분산과 관련이 있다.

Definition (Student's t Distribution)

  • 일단 정의하는 방식부터가 쉽지 않다. Z∼N(0,1), V∼χ2(v)Z \sim N(0,1), \ V \sim \chi^2(v) 에 대해, 다음이 따르는 분포가 t 분포라고 정의한다.

    t=ZV/v∼t(v)t=\frac{Z}{\sqrt{V/v}} \sim t(v)

    • 즉, 표준 정규분포를 따르는 확률변수를 적당히(=카이제곱 분포를 따르는 확률변수와 그 분포의 자유도를 이용해서) scale해주면 t 분포라는 특정 확률 분포를 따른다는 것이다.
    • 그렇다면, 우리가 어떤 실험을 하며 어떤 표본을 구했든, 표준 정규분포를 따르는 값과 카이제곱 분포를 따르는 값을 적당히 구해낸 후, 잘 스케일링 해서 statistic을 구하면, 그 statistic은 t 분포를 따르는 값이라고 볼 수 있다.
    • 그리고 t 분포는 우리가 표본 추출을 통해 구한 어떠한 평균값을 이용한 검정을 하는 데에 쓰인다.

  • 그런데 어떤 표본으로부터 구한 아무 통계량이나 다 표준 정규분포를 따를 리는 만무하다. Sample mean을 standardize해주면 표준 정규분포를 따르게 할 수 있으니, 위 식에 Z=X‾−μσ/nZ=\frac{\overline{X}-\mu}{\sigma / \sqrt{n}} 를 대입한다.

    • 저 우변이 어떻게 표준정규분포를 따르게 되는지는 따로 증명이 있다고 하나 아직 모르겠다.. CLT처럼 n이 발산하는 경우와는 다르고, XiX_i가 애초에 정규분포를 따르는 집단에서 샘플링 되었다는 가정이 있어 가능하다고 한다.

  • 그리고 VV 에는 (n−1)s2σ2\frac{(n-1)s^2}{\sigma^2} 를 대입한다. (n−1)s2σ2\frac{(n-1)s^2}{\sigma^2} 역시 χ2(n−1)\chi^2(n-1)를 따른다.

    • (n−1)s2σ2\frac{(n-1)s^2}{\sigma^2} 가 χ2(n−1)\chi^2(n-1)를 따른다는 것에 대한 증명도 있지만 내용은 아직 모르겠다.

  • 그럼 t=ZV/v=X‾−μσ/n(n−1)s2σ2v=X‾−μsnt=\frac{Z}{\sqrt{V/v}}=\frac{\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}}{\sqrt{\frac{\frac{(n-1)s^2}{\sigma^2}}{v}}}=\frac{\overline{X}-\mu}{\frac{s}{\sqrt{n}}} 이 된다.

    • μ\mu는 모평균, ss는 표본 분산, v=n−1v=n-1이다.

  • 즉 우리가 표본으로부터 구할 수 있는 값인 표본평균, 표본 분산, 표본 개수를 대입하고, 모평균 값은 귀무가설에 따라 대입해서 t-statistic을 계산할 수 있다. 그렇게 계산한 t=X‾−μsnt=\frac{\overline{X}-\mu}{\frac{s}{\sqrt{n}}} 역시 자유도가 n−1n-1인 t 분포 t(n−1)t(n-1)을 따른다.

t-statistic

t-statistic to compare two sample means

  • ZV/v\frac{Z}{\sqrt{V/v}} 에 Z=X1‾−X2‾σ1n1+1n2,V=(n1+n2−2)S2σ2Z=\frac{\overline{X_1}-\overline{X_2}}{\sigma \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}, V=\frac{(n_1+n_2-2)S^2}{\sigma^2} 를 대입한 것과 같다.

    • Z=X1‾−X2‾σ1n1+1n2Z=\frac{\overline{X_1}-\overline{X_2}}{\sigma \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} 가 standard normal distribution을 따른다는 것에 대해 더 살펴보면, 일단 이 경우는 평균이 다르고 분산은 같은 두 분포에서 각각 샘플을 추출했다고 가정한 경우이다. 즉 X1‾∼N(μ1,σ2n1),X2‾∼N(μ2,σ2n2)\overline{X_1} \sim N(\mu_1, \frac{\sigma^2}{n_1}), \quad \overline{X_2} \sim N(\mu_2, \frac{\sigma^2}{n_2}) 이다.

    • 이때 두 sample mean의 분포를 생각해보면, X1‾−X2‾∼N(μ1−μ2,σ2n1+σ2n2)\overline{X_1}-\overline{X_2} \sim N(\mu_1 - \mu_2, \frac{\sigma^2}{n_1} + \frac{\sigma^2}{n_2}) 이다. (두 sample은 독립이라 가정해서 분산은 단순한 합으로 나타내진다.)

    • 이걸 standardize하면 되는데, null hypothesis에서는 μ1=μ2\mu_1 = \mu_2 이라 가정하니 소거된다.

  • 그럼 t-statistic은 t=X1‾−X2‾S1n1+1n1where S=(n1−1)S12+(n2−1)S22n1+n2−2t=\frac{\overline{X_1}-\overline{X_2}}{S \sqrt{\frac{1}{n_1}+\frac{1}{n_1}}} \quad \text{where} \ S = \sqrt{\frac{(n_1 - 1)S_1^2 + (n_2 - 1)S_2^2}{n_1 + n_2 - 2}} 이 된다.

t-statistic of OLS Estimator β^j\hat{\beta}_j

y=Xβ+εy = X\beta + \varepsilon 에 대한 OLS estimator β^j\hat{\beta}_j 에 대해 검정할 때 t-statistic은 t=β^j−cs.e.(β^)jt=\frac{\hat{\beta}_j-c}{s.e.(\hat{\beta})_j} 와 같이 구한다. 이것이 t 분포의 정의에 등장하는 ZV/v\frac{Z}{\sqrt{V/v}} 와 어떻게 같은지 알아보자. β^j\hat{\beta}_j 의 경우에는 Z,VZ, V 각각이 어떤 형태로 들어가야 할지 생각해보면,

  1. Standardization of β^j\hat{\beta}_j

  • β^j\hat{\beta}_j 역시 N(βj,σ2[X′X]jj)N(\beta_j, \frac{\sigma^2}{[X'X]_{jj}}) 라는 정규분포를 따르는 확률변수다. 따라서 β^j\hat{\beta}_j 모평균 βj\beta_j 를 뺀 후 모표준편차 σ2[X′X]jj\sqrt{\frac{\sigma^2}{[X'X]_{jj}}} 로 나눠주면 표준 정규분포를 따르는 확률변수가 된다.

  • 다만 모평균의 자리에는 추후 가설에 따라 다양한 값이 들어갈 수 있으니 cc 로 나타내면, Z=β^j−cσ1[X′X]jjZ=\frac{\hat{\beta}_j-c}{\sigma\sqrt{\frac{1}{[X'X]_{jj}}}} 를 사용하면 된다.

    • 분모에 σ^\hat{\sigma} 가 아닌 σ\sigma 가 온다는 것은 중요한 포인트이다. 모포준편차가 뭔지 몰라도 일단 모표준편차로 나눈다고 보아야 저 값이 표준 정규분포를 따를 수 있기 때문이다.
  1. Xi-squared distributed r.v. from ε\varepsilon

  • VV 자리에 카이제곱 분포를 따르는 확률변수가 들어가야 한다. 기본적으로는 표본분산을 구해서 (n−1)s2σ2\frac{(n-1)s^2}{\sigma^2} 를 대입하게 되는데, OLS Estimator에 대해서는 표본분산 ss 대신 standard error를 이용한다.

  • 결론은, (n−k)σ^2σ2∼χ2(n−k)\frac{(n-k)\hat{\sigma}^2}{\sigma^2} \sim \chi^2(n-k) 를 VV 대신 이용한다. 저렇게 되는 이유는 다음과 같다.

    • 먼저, residual u^\hat{u} 가 정규분포를 따름을 보일 수 있다.
    μ^=y−Xβ^=Xβ+ε−Xβ^=X(β−β^)+ε=X(β−(X′X)−1X′y)+ε=X(β−(X′X)−1X′(Xβ+ε))+ε=X(β−(X′X)−1X′Xβ−(X′X)−1X′ε)+ε=−X(X′X)−1X′ε+ε=(I−H)ε(where H is hat matrix)\scriptsize \begin{aligned} \hat{\mu} & = y - X \hat{\beta} \\ & = X \beta + \varepsilon - X \hat{\beta} \\ & = X ( \beta - \hat{\beta} ) + \varepsilon \\ & = X ( \beta - (X'X)^{-1}X'y ) + \varepsilon \\ & = X ( \beta - (X'X)^{-1}X'(X \beta + \varepsilon) ) + \varepsilon \\ & = X ( \beta - (X'X)^{-1}X'X \beta - (X'X)^{-1}X' \varepsilon ) + \varepsilon \\ & = -X (X'X)^{-1}X' \varepsilon + \varepsilon \\ & = (I-H) \varepsilon && \text{(where $H$ is hat matrix)} \\ \end{aligned}

    • 그리고 ε∼N(0,σ2I)\varepsilon \sim N(0, \sigma^2 I) 가정이 있으므로, u^∼N(0,σ2(I−H))\hat{u} \sim N(0, \sigma^2(I-H)) 로 residual u^\hat{u} 역시 정규분포를 따른다.

    • 그럼 정규분포를 따르는 u^\hat{u} 는 제곱하면 카이제곱 분포를 따르게 되므로, u^′u^σ2∼χ2(n−k)\frac{\hat{u}'\hat{u}}{\sigma^2} \sim \chi^2(n-k) 이다. (자유도가 n-k인 카이제곱을 따르는 구체적인 이유는?)

    • 그리고 정의에 따라 σ^2=u^′u^n−k\hat{\sigma}^2=\frac{\hat{u}'\hat{u}}{n-k} 이므로, (n−k)σ^2σ2∼χ2(n−k)\frac{(n-k)\hat{\sigma}^2}{\sigma^2} \sim \chi^2(n-k) 가 된다.

  1. 정리

t=ZV/vt=\frac{Z}{\sqrt{V/v}} 에 Z=β^j−cσ1[X′X]jj,V=(n−k)σ^2σ2,v=n−kZ=\frac{\hat{\beta}_j-c}{\sigma\sqrt{\frac{1}{[X'X]_{jj}}}}, V=\frac{(n-k)\hat{\sigma}^2}{\sigma^2}, v=n-k 를 대입하면 t=β^j−cσ1[X′X]jj(n−k)σ^2σ2n−k=β^j−cσ^2[X′X]jj=β^j−cs.e.(β^)jt=\frac{\frac{\hat{\beta}_j-c}{\sigma\sqrt{\frac{1}{[X'X]_{jj}}}}}{\sqrt{\frac{\frac{(n-k)\hat{\sigma}^2}{\sigma^2}}{n-k}}} = \frac{\hat{\beta}_j-c}{\sqrt{\frac{\hat{\sigma}^2}{[X'X]_{jj}}}} = \frac{\hat{\beta}_j-c}{s.e.(\hat{\beta})_j} 와 같다.

Test

이제 우리가 구한 통계량이 통계적으로 유의미한지 검정을 할 때 t-statistic 값을 이용할 수 있다.

Null/Alternative Hypothesis의 의미

H0:β^j≤c, H1:β^j>cH_0: \hat{\beta}_j \leq c, \ H_1: \hat{\beta}_j > c 에 대해 검정하는 one-tailed test 상황을 예시로 하여, t-test에 대해 알아보자.

  • 우리는 수집한 데이터를 이용해 β^j\hat{\beta}_j 라는 값을 구했다. 우리는 이 값이 여러 측면에서 통계적으로 유의미한지 검정해보고 싶은 것이다.

    • 예를 들어 β^j\hat{\beta}_j 의 값이 0과 (통계적으로 유의미하게) 다르다고 말할 수 있는지(=H1:β^j≠0H_1: \hat{\beta}_j \ne 0), 또는 β^j\hat{\beta}_j 의 값이 3보다 (통계적으로 유의미하게) 크다고 말할 수 있는지(=H1:β^j>3H_1: \hat{\beta}_j > 3) 궁금할 수 있다.

    • 대립가설이 H1:β^j>cH_1: \hat{\beta}_j > c 와 같은 형태라고 해서 'β^j\hat{\beta}_j 의 값이 실제로 c보다 큰지 따져보겠다' 라는 의미로 생각하면 이해가 힘들어진다. 어떠한 부등식을 세워놓고(=귀무가설 β^j≤c\hat{\beta}_j \leq c), 그게 틀렸다고 볼 통계적으로 유의미한 증거가 있는지 따져보는 것이다. (애초에 부등식 자체는 항상 성립한다. 구해진 β^j\hat{\beta}_j 값보다 작은 값을 cc 에 넣을테니까)

Significance Level의 의미

  • '귀무 가설을 기각할 (통계적으로 유의미한) 증거가 있는지' 따지는 방식은, β^j\hat{\beta}_j 의 실제 값인 βj\beta_j 의 값을 일단 적당히 가정한 후, 우리가 구한 β^j\hat{\beta}_j 의 값이 관측될 법한 값인지 따져본다.

  • '관측될 법한 값인지'를 따지는 방법은 t-분포를 이용하는 것이다. OLS Estimator의 t-statistic은 β^j\hat{\beta}_j 과 βj\beta_j 값을 필요로 하니, 각각에 값을 집어 넣은 후 그 t-statistic이 따르는 t 분포에서 그 t-statistic이 나올 법 한지 따져보면 된다.

    • βj\beta_j 값을 적당히 상정해서 계산한 t-statistic은, 귀무가설이 맞다고 가정하고 구한 값이라고 볼 수 있다.
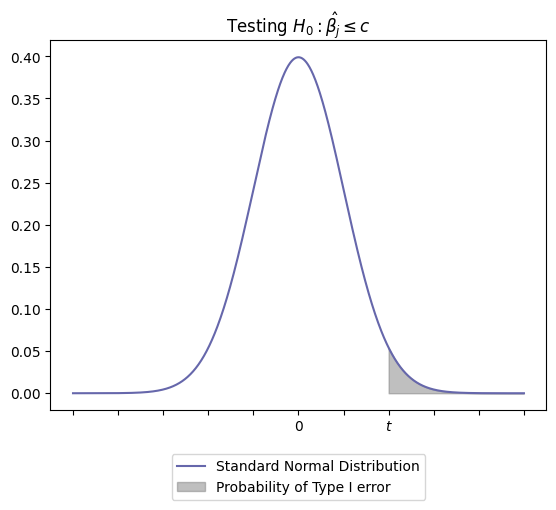
after_standardize

  • 시각화해서 보면, t-statistic의 값이 어떻게 나오든 언제나 위와 같은 종모양의 t-분포를 따를 것이다.

    • 사실 t-statistic의 값이 t 분포의 어느 곳에 위치하더라도, 그 t-statistic이 해당 t 분포로부터 나왔을 확률이 0은 아닐 것이다. 하지만 확률 분포이니, 아무래도 t-statistic이 0 근처라면 상대적으로 더 일어날 법한 일이라고 생각할 수 있다. 즉 귀무 가설이 일어날 법한 일이라는 의미로 생각할 수 있다.
    • 반대로 t-statistic의 값이 0으로부터 멀리 떨어져있을 수록 그 t-statistic 값은 그것이 따르는 t-분포에서 나왔다고 보기 어려울 것이다. 즉 귀무 가설이 일어날 법한 일이 아니므로 기각하게 된다. (이는, 어떤 통계량들의 차이가 수집된 데이터 내의 산포도로 인한 차이보다 커야 한다는 직관과도 부합한다.)
    • 그러니 t 분포의 끝자락에 해당하는 값이 나오면, 귀무 가설을 그냥 기각해버린다는 것이 핵심 아이디어이다. t 분포의 한쪽 끝자락 5%의 구간에나 해당하는 t-statistic 값이 계산됐다면, 그걸 '끝자락에서 나올 정도로 일어날 가능성이 낮지만 그럼에도 이건 일어날 법한 일이다!' 라고는 하지 않는다는 것이다.
    • 그래서 얼마나 끝자락에서 t-statistic 값이 나오면 귀무 가설을 기각할지 기준을 정하고, 그게 significance level(α\alpha)이다. 끝자락 α\alpha %에 해당하는 구간에서 t-statistic 값이 나오면, 1종 오류(Type I Error)가 일어나도 신경쓰지 않겠다는 식으로 귀무가설을 기각한다.
      • 이게 왜 1종 오류와 관련이 있는 건가 했는데, 일단 가설 검정에 있어 1종 오류는 H0H_0 이 맞지만 H0H_0 을 기각해버리는 경우를 말한다.
      • 상기했듯 t-statistic을 구하는 것 자체가 Null Hypothesis H0H_0 를 맞다고 보는 것이다. 그런데도 H0H_0 를 기각해버리는 것은 1종 오류와 같다.
      • 대신, t-statistic의 값이 0으로부터 상당히 떨어져있을 때에 생기는 1종 오류는 어차피 잘 일어나지 않을 법한 일이니, 전체에서 끝자락 α\alpha % 만큼의 확률로 일어나는 1종 오류는 용인하는 것이다.
    • α\alpha 의 크기는 보통 0.1, 0.05, 0.01을 사용한다. SURF Reading Group에서 읽었던 (Reinartz et al., 2016.)에서도 그랬다.

  • 따라서, 검정은 보통 아래의 둘 중 하나와 같이 이루어진다.

    1. t-statistic의 값이 critical value보다 바깥에 있거나
    2. 위 그림에서 회색 영역에 해당하는 부분의 넓이 p-value가 유의 수준(significance level)보다 낮으면 된다. (회색 영역의 넓이가 작아진다는 것은 0으로부터 멀어진다는 뜻이니까 1과 같은 내용.)

One-tailed test

는 H0:β^j≤c, H1:β^j>cH_0: \hat{\beta}_j \leq c, \ H_1: \hat{\beta}_j > c 와 같이 대립가설에 부등식이 있는 경우이다.

Two-tailed test

는 H0:β^j=c, H1:β^j≠cH_0: \hat{\beta}_j = c, \ H_1: \hat{\beta}_j \ne c 와 같이 대립가설에 부등호 있는 경우가 해당된다. β^j≠c\hat{\beta}_j \ne c 는 β^j<corβ^j>c\hat{\beta}_j < c \quad \text{or} \quad \hat{\beta}_j > c 와 같으므로, t 분포의 양쪽 끝자락에 각각 α2\frac{\alpha}{2} 만큼의 significance level을 지정한다.



2024.08.29

References

https://blog.naver.com/mykepzzang/220852102307
http://infoso.kr/?p=2920
그리고 ChatGPT와의 수많은 대화