Rejection sampling

Rejection Sampling

Rejection Sampling은 특정 확률분포로부터 샘플링을 하기 위한 Monte Carlo 방법의 일종이다.

가령 다음과 같이 3개의 정규 분포를 합하여 만들어진 PDF로부터 샘플링을 하려면 어떻게 해야 할까?

\footnotesize \begin{aligned} p(x) = 0.5 \cdot \frac{1}{0.75 \sqrt{2\pi}} e^{- \frac{1}{2}(\frac{x-3}{0.75})^2} + 0.25 \cdot \frac{1}{0.5 \sqrt{2\pi}} e^{- \frac{1}{2}(\frac{x-1}{0.5})^2} + 0.25 \cdot \frac{1}{1.0 \sqrt{2\pi}} e^{- \frac{1}{2}(\frac{x-2}{1.0})^2} \end{aligned}

먼저 쉽게 샘플링을 할 수 있는 확률 분포를 proposal distribution $g(x)$ 를 준비한다. 예를 들어 정규 분포를 사용할 수 있다.

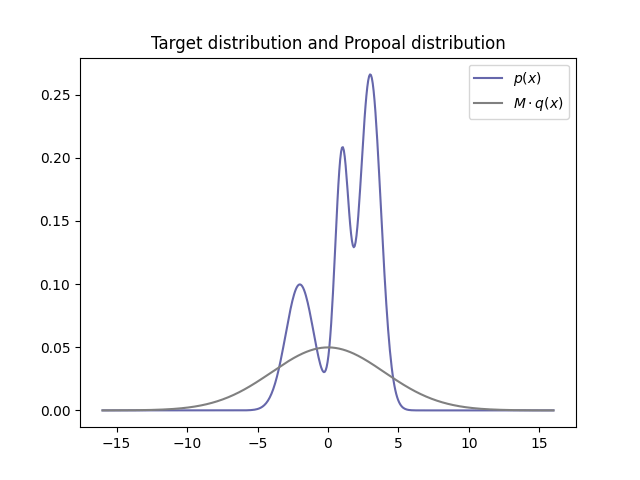
위 그림의 회색이 정규 분포의 $q(x)=\frac{1}{4.0 \sqrt{2\pi}} e^{- \frac{1}{2}(\frac{x-3}{4.0})^2}$ 의 pdf이다.

그리고 이 proposal distribution $q(x)$ 와 x축 사이의 영역에 target distribution의 pdf가 모두 들어오도록 적당한 상수 $M$ 을 곱해준다.

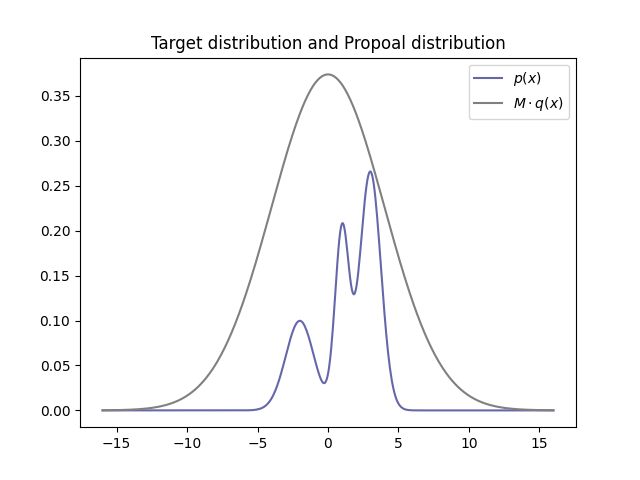
이 경우 $M=7.5$ 를 곱해주면 $p(x)$ 가 모두 $7.5 \cdot q(x)$ 의 아래에 들어오게 된다.

그리고 다음 과정을 거쳐 샘플링을 진행한다.

proposal distribution $q(x)$ 에서 하나의 값을 $x^*$ 를 샘플링한다.
$p(x^*)$ 와 $M q(x^*)$ 를 계산하고, acceptance probability $\frac{p(x^*)}{M q(x^*)}$ 를 계산한다.
$u \sim \text{Unif}(0, 1)$ 를 샘플링한다.
$u \leq \frac{p(x^*)}{M q(x^*)}$ 이면 $x^*$ 를 Accept, 아니면 Reject한다.

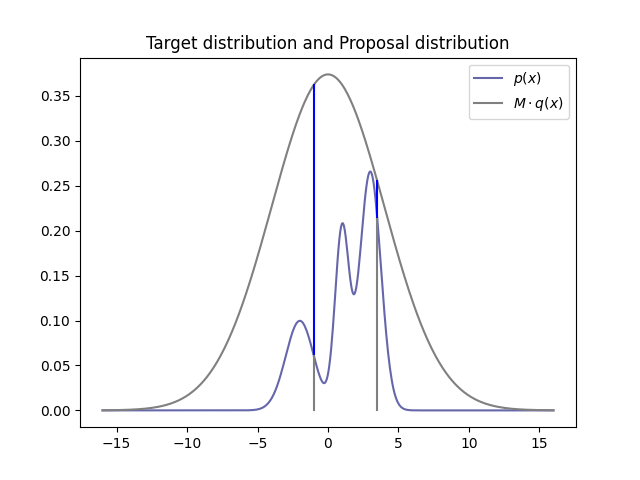
proposal distribution으로부터 특정 $x^*$ 값을 일단 뽑아낸 후, 그 지점에서 proposal distribution과 target distribution의 값의 비에 따라서 해당 $x^*$ 값을 샘플링의 결과에 포함시킬지 여부가 결정된다.

$u$ 를 $\text{Unif}(0, 1)$ 로부터 샘플링하고, proposal distribution과 target distribution 비율의 범위도 $[0, 1]$ 의 범위에 들어가게 되니, 둘의 비율이 곧 그 $x^*$ 를 accept하게 되는 확률이 된다.

위의 그림에서는

$x^* = -1$ 이면 $\frac{p(x^*)}{M q(x^*)}=0.167$
$x^* = 3.5$ 이면 $\frac{p(x^*)}{M q(x^*)}=0. 835$

으로 차이가 남을 알 수 있는데, 이렇듯 샘플이 더 많이 나와야 할 구간에서는 acceptance probability가 높아져 더 많은 샘플이 accept되며 샘플링이 이루어진다.

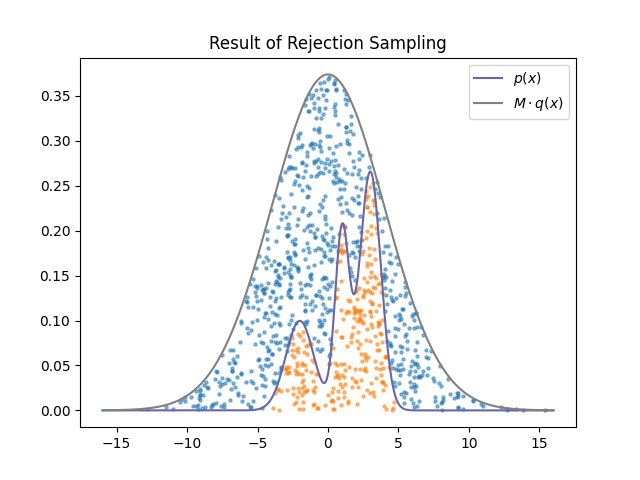
위 그림은 $N=1000$ 으로 샘플링 후 285회의 accept, 715회의 reject가 발생한 결과이다. 파란색 점들이 찍힌 영역에서는 reject, 주황색 점들이 찍힌 영역에서는 accept됨을 시각적으로 확인할 수 있다.

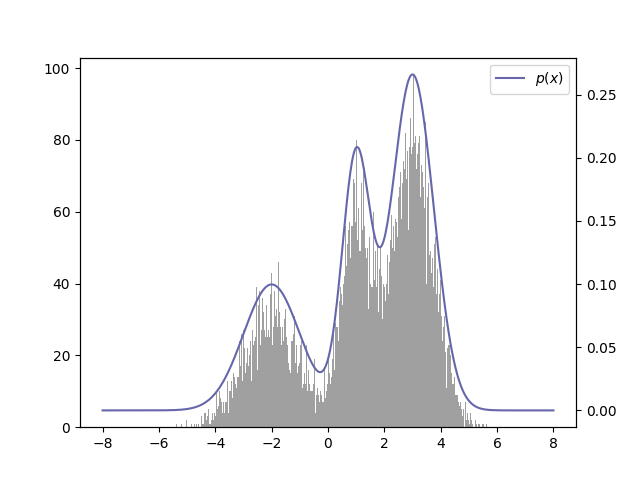
샘플링된 $x$ 값들을 히스토그램으로 나타내면 이런 모습이 된다.

import numpy as np
import matplotlib.pyplot as plt

def target_distribution(x):
    return 0.5 * np.exp(-0.5 * ((x - 3) / 0.75) ** 2) / (0.75 * np.sqrt(2 * np.pi)) + \
           0.25 * np.exp(-0.5 * ((x - 1) / 0.5) ** 2) / (0.5 * np.sqrt(2 * np.pi)) + \
           0.25 * np.exp(-0.5 * ((x + 2) / 1.0) ** 2) / (1.0 * np.sqrt(2 * np.pi))

def proposal_distribution(x):
    return 7.5 * (0.5 * np.exp(-0.5 * ((x) / 4.0) ** 2) / (4.0 * np.sqrt(2 * np.pi)))

SEED = 100
N = 50000

np.random.seed(SEED)

if __name__ == "__main__":
    data_x_accepted, data_y_accepted, data_x_rejected, data_y_rejected = [[] for _ in range(4)]

    max_y = proposal_distribution(0)

    for i in range(N):
        j = np.random.normal(0, 4)
        u = np.random.uniform(0, 1)

        target = target_distribution(j)
        proposal = proposal_distribution(j)

        if u <= (target/proposal):
            data_x_accepted.append(j)
            data_y_accepted.append(u*proposal_distribution(j))
        else:
            data_x_rejected.append(j)
            data_y_rejected.append(u*proposal_distribution(j))


    # Plot sampled points
    # print("# of accepted points =", len(data_x_accepted))
    # print("# of rejected points =", len(data_x_rejected))
    # plt.scatter(data_x_rejected, data_y_rejected, s=5, alpha=0.5)
    # plt.scatter(data_x_accepted, data_y_accepted, s=5, alpha=0.5)

    # Plot PDFs
    # plt.title('Result of Rejection Sampling')
    # x = np.linspace(-16, 16, 500)
    # y_1 = target_distribution(x)
    # y_2 = proposal_distribution(x)
    # plt.plot(x, y_1, color="#6667ab", label=r"$p(x)$")
    # plt.plot(x, y_2, color="gray", label=r"$M \cdot q(x)$")

    # Plot additional vertical line
    # x_1_plot, x_2_plot = -1, 3.5
    # plt.plot([x_1_plot, x_1_plot], [target_distribution(x_1_plot), proposal_distribution(x_1_plot)],
    #                                 linestyle='-', color='blue')
    # plt.plot([x_1_plot, x_1_plot], [0, target_distribution(x_1_plot)], linestyle='-', color='gray')

    # plt.plot([x_2_plot, x_2_plot], [target_distribution(x_2_plot), proposal_distribution(x_2_plot)],
    #                                 linestyle='-', color='blue')
    # plt.plot([x_2_plot, x_2_plot], [0, target_distribution(x_2_plot)], linestyle='-', color='gray')

    # Calculate acceptance probability
    # print("Acceptance probability of x_1 =",
    #       target_distribution(x_1_plot)/ proposal_distribution(x_1_plot))
    # print("Acceptance probability of x_2 =",
    #       target_distribution(x_2_plot)/ proposal_distribution(x_2_plot))

    # Plot histogram using both y-axes
    x = np.linspace(-8, 8, 500)
    plt.hist(data_x_accepted, bins=500, color="gray", alpha=0.75)

    ax_2 = plt.twinx()
    y_1 = target_distribution(x)
    y_2 = proposal_distribution(x)
    ax_2.plot(x, y_1, color="#6667ab", label=r"$p(x)$")

    # Visualize
    plt.legend()
    plt.savefig('./result.png')
    plt.show()

2025.01.19