Home
Blog
Music
Photo

Markov Chain Monte Carlo

Tags:
MCMCMonte Carlo

Markov Chain Monte Carlo

Transition Distribution

Markov Chain에서와 동일한 예시를 사용하였다.

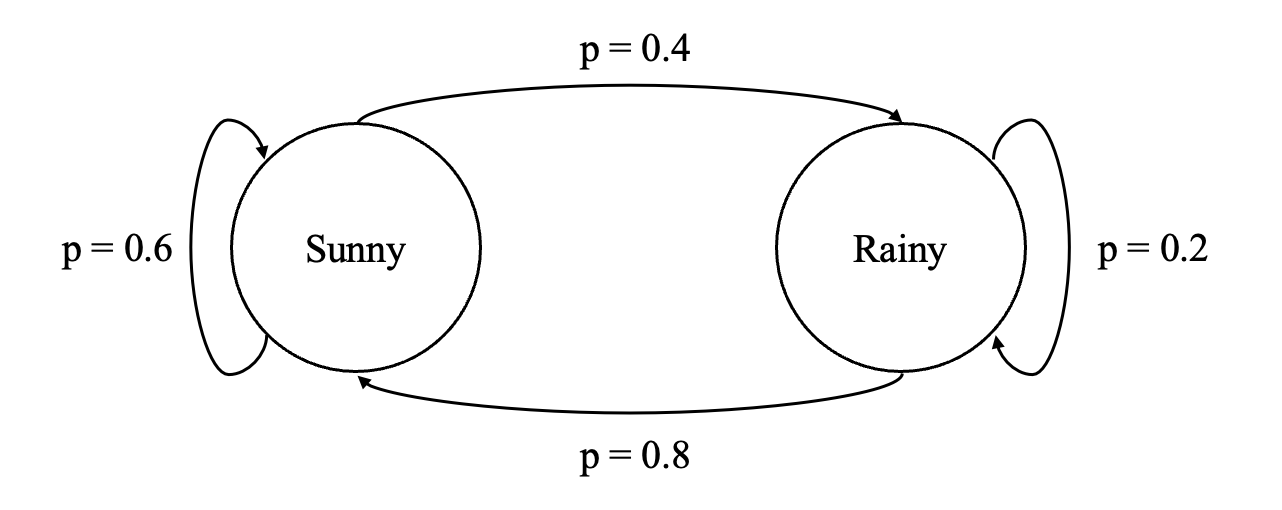
markov_chain

위 예시의 Markov chain이 가지는 Transition matrix는

[0.60.40.80.2]=[(Sunny→Sunny)(Sunny→Rainy)(Rainy→Sunny)(Rainy→Rainy)]=t+1t+1SunnyRainytSunny0.60.4tRainy0.80.2\scriptsize \begin{aligned} \begin{bmatrix} 0.6 & 0.4 \\ 0.8 & 0.2 \\ \end{bmatrix} &= \begin{bmatrix} (\text{Sunny} \rightarrow \text{Sunny}) & (\text{Sunny} \rightarrow \text{Rainy}) \\ (\text{Rainy} \rightarrow \text{Sunny}) & (\text{Rainy} \rightarrow \text{Rainy}) \\ \end{bmatrix} \\ &= \begin{array}{|c|c|c|c|} \hline & & t+1 & t+1 \\ \hline & & \text{Sunny} & \text{Rainy} \\ \hline t & \text{Sunny} & 0.6 & 0.4 \\ \hline t & \text{Rainy} & 0.8 & 0.2 \\ \hline \end{array} \end{aligned}

와 같고, 이때 Transition distribution T(xj∣xi)T(x_j \vert x_i) 는

T(Sunny∣Sunny)=0.6T(Rainy∣Sunny)=0.4T(Sunny∣Rainy)=0.8T(Rainy∣Rainy)=0.2\footnotesize \begin{aligned} T(\text{Sunny} \vert \text{Sunny}) = 0.6 \\ T(\text{Rainy} \vert \text{Sunny}) = 0.4 \\ T(\text{Sunny} \vert \text{Rainy}) = 0.8 \\ T(\text{Rainy} \vert \text{Rainy}) = 0.2 \\ \end{aligned}

이다.


Stationary distribution

위의 Transition matrix PP 에 대해 π P=π\pi \ P = \pi 를 만족시키는, 즉 Transition을 거쳐도 변화가 없는 상태를 Stationary distribution 이라고 한다.

위 Transition matrix에 대해 stationary distribution은 π=[23,13]\pi=[\frac{2}{3}, \frac{1}{3}] 이다.

(PP 를 여러 번 곱하다보면 더이상 변하지 않게 되는 상태를 의미하는 Steady-state과 유사)


Detailed Balance

Detailed balance는 두 state i,ji, j를 오가는 확률이 서로 동일함을 의미한다.

p(xi)T(xj∣xi)=p(xj)T(xi∣xj)p(x_i) T(x_j \vert x_i) = p(x_j) T(x_i \vert x_j)

즉 두 state에 대하여 특정 state에 있을 확률과 그 state에서 다른 state로 이동할 확률이 서로 같음을 의미한다.

Detailed balance가 만족될 경우 Stationary distirubtion의 존재가 보장된다.


Metropolis-Hastings

MH 알고리즘의 목적은 Markov Process를 디자인하는 것이다.

Stationary distribution이 target distribution p(x)p(x) 이 되는 Markov chain을 찾는 것을 목표로 한다.

  • target distribution p(x)p(x) 가 있고

  • proposal distribution q(x′∣x)q(x' \vert x) 를 도입. t−1t-1 시점의 state xx 로부터 다음 tt 시점의 state x′x'를 제안한다. 가령 정규 분포 N(x,σ2)\mathcal{N}(x, \sigma^2) 를 사용할 수 있다.

  • Acceptance distribution A(x′,x)A(x', x) 를 정의한다. x′x' 가 accept될 확률을 의미한다.

  • 그렇다면 T(x′∣x)=q(x′∣x)A(x′,x)T(x' \vert x) = q(x' \vert x) A(x', x), 즉 state xx 에서 state x′x' 로 넘어갈 확률은 (state xx 에서 state x′x'를 제안할 확률) * (acceptance의 확률) 이라는 관계가 생긴다.

  • Transition distribution T(x′∣x)T(x' \vert x) 는 항상 알고 있는 것이 아니므로 위 detailed balance 식을 이용해 제거한다.

p(xi)T(xj∣xi)=p(xj)T(xi∣xj)p(xi)p(xj)=T(xi∣xj)T(xj∣xi)p(x′)p(x)=q(x′∣x)A(x′,x)q(x∣x′)A(x,x′)\footnotesize \begin{aligned} p(x_i) T(x_j \vert x_i) &= p(x_j) T(x_i \vert x_j) \\ \frac{p(x_i)}{p(x_j)} &= \frac{T(x_i \vert x_j)}{T(x_j \vert x_i)} \\ \frac{p(x')}{p(x)} &= \frac{q(x' \vert x) A(x', x)}{q(x \vert x') A(x, x')} \\ \end{aligned}

Acceptance distribution들에 대해 정리하면

A(x′,x)A(x,x′)=p(x′)q(x∣x′)p(x)q(x′∣x)\footnotesize \begin{aligned} \frac{A(x', x)}{A(x, x')} &= \frac{p(x') q(x \vert x')}{p(x) q(x' \vert x)} \\ \end{aligned}

(Metropolis 알고리즘은 symmetric transition matrix를 가정하므로 q(x′∣x)=q(x∣x′)q(x' \vert x)=q(x \vert x') 이기 때문에 A(x′,x)A(x,x′)=p(x′)p(x)\frac{A(x', x)}{A(x, x')} = \frac{p(x')}{p(x)} 로 쓴다.)

이제 위 식이 성립하도록 acceptance distribution을 정하면 된다. 이때 주로 사용되는 방법은 Metropolis choice:

A(x′,x)=min(1,p(x′)q(x∣x′)p(x)q(x′∣x))\footnotesize \begin{aligned} A(x', x) &= \text{min} \left(1, \frac{p(x') q(x \vert x')}{p(x) q(x' \vert x)} \right) \\ \end{aligned}

이렇게 acceptance distribution을 정의하면, A(x′,x)A(x', x) 나 A(x′,x)A(x', x) 중 하나는 1이 된다.

  1. p(x′)q(x∣x′)p(x)q(x′∣x)≥1 \frac{p(x') q(x \vert x')}{p(x) q(x' \vert x)} \geq 1, 즉 새로 제안된 state의 likelihood가 직전 state의 likelihood보다 크면 A(x′,x)=1A(x', x)=1.
  2. p(x′)q(x∣x′)p(x)q(x′∣x)<1 \frac{p(x') q(x \vert x')}{p(x) q(x' \vert x)} < 1, 즉 새로 제안된 state의 likelihood가 직전 state의 likelihood보다 작으면 A(x,x′)=1A(x, x')=1.

샘플링 원리

  • u∼Unif(0,1)u \sim \text{Unif}(0, 1) 를 샘플링 후 α∗=min(1,p(x′)q(x∣x′)p(x)q(x′∣x))\alpha^* = \text{min} \left(1, \frac{p(x') q(x \vert x')}{p(x) q(x' \vert x)} \right) 와 비교하여, u≤α∗u \leq \alpha^* 이면 accept, 아닐 경우에는 reject한다.
  • p(x′)p(x)≥1\frac{p(x')}{p(x)} \geq 1, 즉 새로 제안된 state의 likelihood가 직전 state의 likelihood보다 클수록 p(x′)q(x∣x′)p(x)q(x′∣x)≥1\frac{p(x') q(x \vert x')}{p(x) q(x' \vert x)} \geq 1 이 될텐데, 이 경우에는 α∗=1\alpha^* = 1 이니 새로 제안된 state가 항상 accept된다.
  • p(x′)p(x)<1\frac{p(x')}{p(x)} < 1, 즉 새로 제안된 state의 likelihood가 직전 state의 likelihood보다 작을수록 p(x′)q(x∣x′)p(x)q(x′∣x)<1\frac{p(x') q(x \vert x')}{p(x) q(x' \vert x)} < 1 이 되고, 이 경우에는 α∗=p(x′)q(x∣x′)p(x)q(x′∣x)\alpha^* = \frac{p(x') q(x \vert x')}{p(x) q(x' \vert x)} 이니 p(x′)q(x∣x′)p(x)q(x′∣x)\frac{p(x') q(x \vert x')}{p(x) q(x' \vert x)} 값을 acceptance probability로 가진다.

비대칭성 보정

  • p(x′)p(x)\frac{p(x')}{p(x)} 뒤의 항 q(x∣x′)p(x)q(x′∣x)\frac{q(x \vert x')}{p(x) q(x' \vert x)} 을 통해 proposal distribution의 비대칭에 대한 보정이 이루어진다.
    • 예를 들어 q(x′∣x)>q(x∣x′)q(x' \vert x) > q(x \vert x') 라면, 애초에 proposal distribution은 xx 다음에 x′x' 를 제안할 가능성이 (그 반대에 비해 상대적으로) 높다.
    • 하지만 p(x′)p(x)\frac{p(x')}{p(x)} 에 q(x∣x′)q(x′∣x)\frac{q(x \vert x')}{q(x' \vert x)} 를 곱하기 때문에, acceptance probability를 감소시키는 방식으로 proposal distribution의 비대칭성을 고려한다.

예시

import numpy as np
import matplotlib.pyplot as plt

def target_distribution(x):
    return 0.5 * np.exp(-0.5 * ((x - 3) / 0.75) ** 2) / (0.75 * np.sqrt(2 * np.pi)) + \
           0.25 * np.exp(-0.5 * ((x - 1) / 0.5) ** 2) / (0.5 * np.sqrt(2 * np.pi)) + \
           0.25 * np.exp(-0.5 * ((x + 2) / 1.0) ** 2) / (1.0 * np.sqrt(2 * np.pi))

def proposal_distribution(x_prev, std):
    return np.random.normal(x_prev, std)

SEED = 100
N = 10000
STD = 1.5

np.random.seed(SEED)

if __name__ == "__main__":
    data_x_accepted = []

    x_prev = 0

    for i in range(N):
        u = np.random.uniform(0, 1)

        target = target_distribution(x_prev)
        x_proposal = proposal_distribution(x_prev, STD)

        p_x_star = target_distribution(x_proposal)
        p_x = target_distribution(x_prev)

        acceptance_probability = min(1, p_x_star/p_x)

        if u <= acceptance_probability:
            data_x_accepted.append(x_proposal)
            x_prev = x_proposal

    # Plot histogram and sampled data
    fig, axes = plt.subplots(1, 2, figsize=(12, 5))
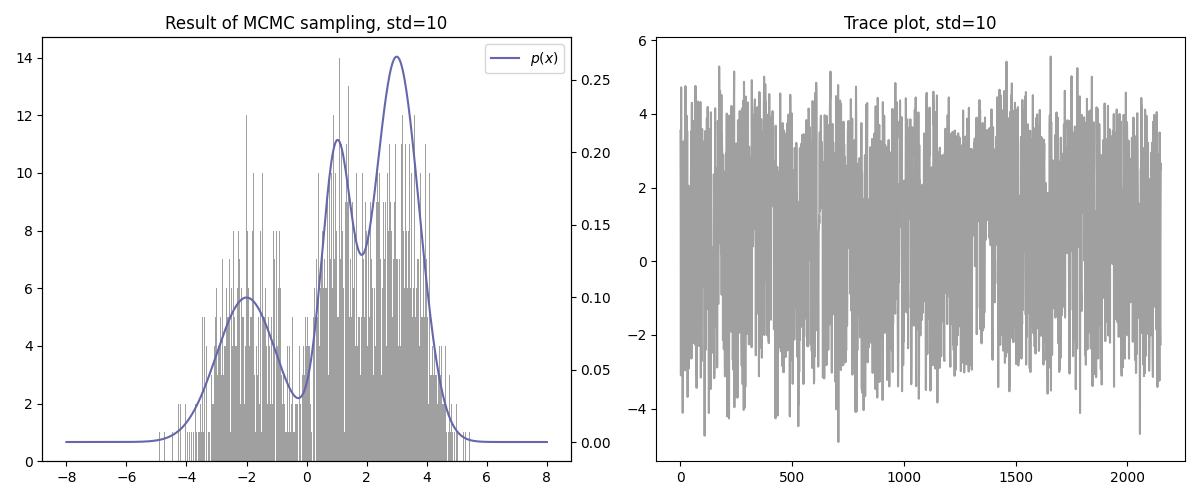
    axes[0].set_title(f"Result of MCMC sampling, std={STD}")
    axes[1].set_title(f"Trace plot, std={STD}")

    axes[0].hist(data_x_accepted, bins=500, color="gray", alpha=0.75)

    ax1_2 = axes[0].twinx()
    x = np.linspace(-8, 8, 500)
    y_1 = target_distribution(x)
    ax1_2.plot(x, y_1, color="#6667ab", label=r"$p(x)$")

    x2 = np.arange(1, len(data_x_accepted)+1)
    axes[1].plot(x2, data_x_accepted, color="gray", alpha=0.75)

    # Visualize
    plt.legend()
    plt.tight_layout()
    plt.savefig(f'./result_std_{str(STD).replace(".", "_")}.png')
    plt.show()
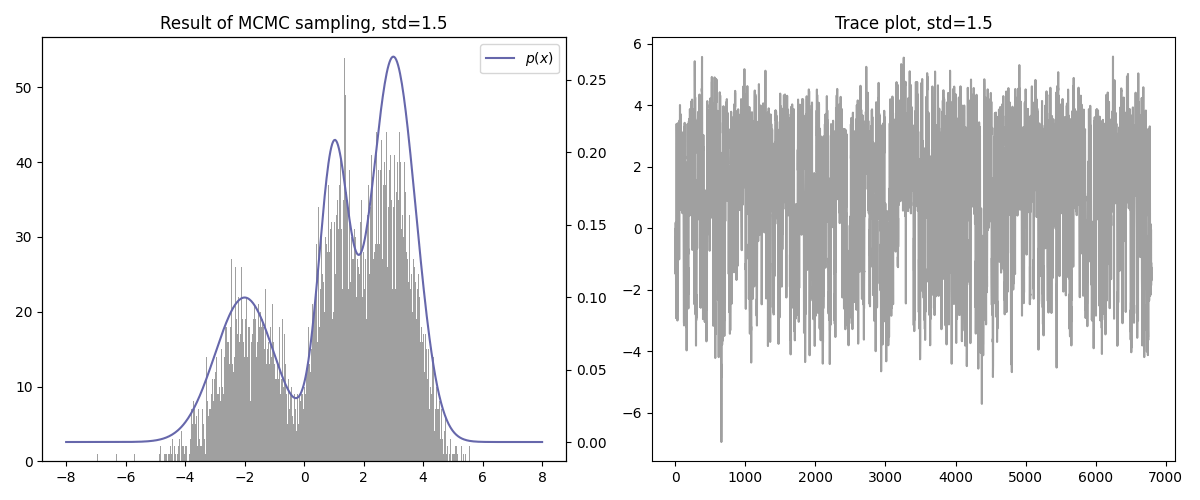
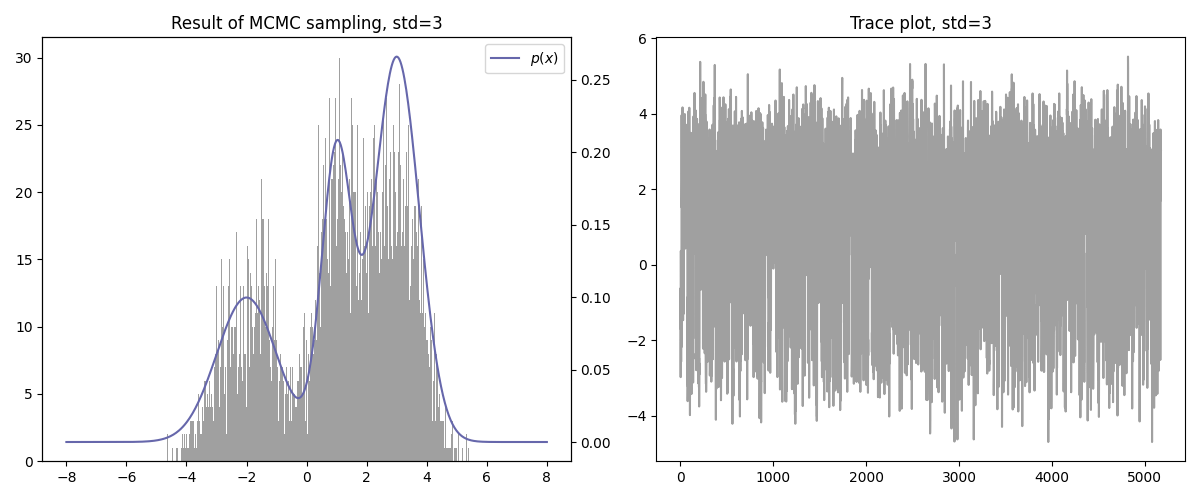
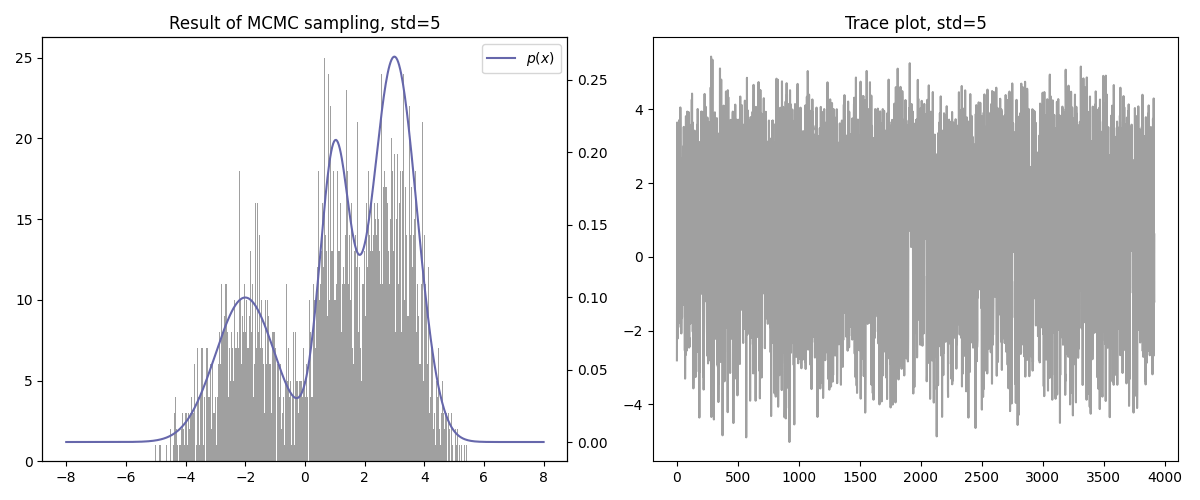
markov_chain markov_chain markov_chain markov_chain

기타

  • 수렴 속도가 빠른 편이다.
  • Curse of dimensionality는 여전히 존재한다.



2025.01.20

Reference

https://infossm.github.io/blog/2019/01/11/mcmc/
https://en.wikipedia.org/wiki/Metropolis–Hastings_algorithm#Formal_derivation
https://harang3418.tistory.com/12