Markov Chain
Markov chain이란
: Markov property를 가지는 Discrete stochastic process
Markov property는 t 시점의 state는 직전 t-1 시점 state만의 영향을 받음을 의미하고, P(Xt+1∣Xt,Xt−1,⋯)=P(Xt+1∣Xt) 와 같이 나타낸다.
Markov matrix와 곱의 의미 (날씨 예시)
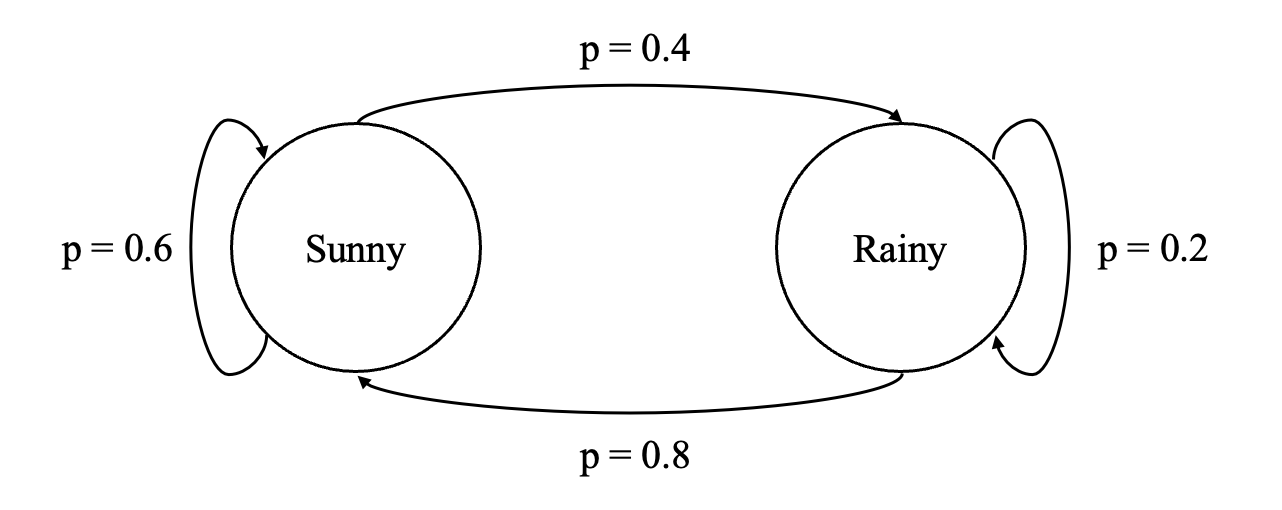 [0.60.80.40.2]=[p(Sunny→Sunny)p(Rainy→Sunny)p(Sunny→Rainy)p(Rainy→Rainy)]=ttSunnyRainyt+1Sunny0.60.8t+1Rainy0.40.2
[0.60.80.40.2]=[p(Sunny→Sunny)p(Rainy→Sunny)p(Sunny→Rainy)p(Rainy→Rainy)]=ttSunnyRainyt+1Sunny0.60.8t+1Rainy0.40.2
와 같은, t 시점과 t+1 시점의 날씨에 대한 확률을 의미를 가지는 Transition matrix가 있을 때,
[0.60.80.40.2][0.60.80.40.2]=[0.680.640.320.36]
와 같이 두 번 곱해준 것은
[p(S→S)p(R→S)p(S→R)p(R→R)][p(S→S)p(R→S)p(S→R)p(R→R)]
=[p(S→S→S)+p(S→R→S)p(R→S→S)+p(R→R→S)p(S→S→R)+p(S→R→R)p(R→S→R)+p(R→R→R)]
즉
ttSunnyRainyt+2Sunny0.680.64t+2Rainy0.320.36
와 같이 t,t+1 일을 거쳐 t+2 일의 날씨에 대한 정보를 담은 행렬이 된다.
t 시점의 날씨에 대한 확률이 맑음 0.3, 흐림 0.7의 확률이었을 때 위 행렬로 t+2 시점의 날씨에 대한 확률을 구하려면
[0.3,0.7][0.60.80.40.2][0.60.80.40.2]=[0.652,0.348]
와 같이 계산할 수 있다.
Transition matrix는 꼭 위와 같은 Markov matrix의 형태인 것은 아니고, 다양한 상태 변화를 표현할 수 있다. (참고)
Hidden Markov Model
참고
2024.02.19
2024.07.04 (HMM)
2025.01.20 (수식에 한글 표기 수정)

